Biomedical Engineering Reference
In-Depth Information
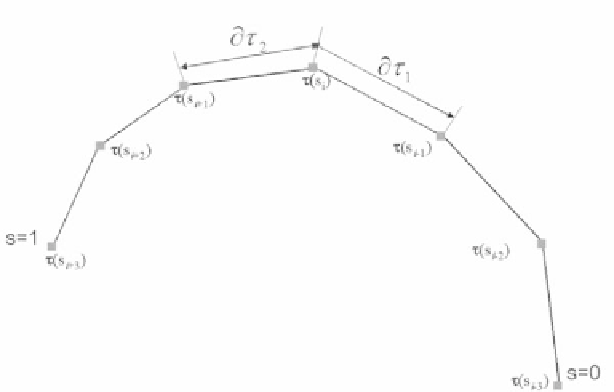
Figure 3.
Illustration of computation of the surface tension and rigidity energies in the
parametric snake framework. See attached CD for color version.
where the first term simulates the tension of the contour and the second, which is
in essence the acceleration term, simulates the rigidity of the contour
τ
(
s
).
α
(
s
)
and
β
(
s
) (
α
(
s
)
,β
(
s
)
∈
[0
,
1]) are the controlling strengths associated with the
surface tension and rigidity terms. Although the strength factors are expressed
as functions of the parameter
s
, in most cases they remain constant throughout
the contour length. Thus, the term
s
will be dropped in future references to these
factors for simplification.
Let us see how these terms control the contour behavior as the total energy
functional tries to minimize itself. The first order derivative term in Eq. (2) can be
minimized by reducing the value of the numerator. Thus, the difference between
the two points
∂
needs to be reduced (see Figure 3), which leads to shrinking the
length of the contour
τ
τ
(
s
). On the other hand, the second term in the expression
is by definition the curvature term. Reduction of that term means the difference
between
∂
τ
2
in Figure 3 needs to be minimized. Thus, minimizing this
term leads to resistance to any bending and eventually straightening the contour
τ
(
s
), leading to a smooth contour. In case the contour is a closed one, the effect
of these two terms will lead to a shrinking circle, in the absence of any other force.
Once the physical constraints are defined, the behavior of the contour is well
set in terms of its geometric properties. However, its behavior on the image domain
needs to be controlled by the image statistics-driven factors, such that the local
minima coincide with the image feature of interest. For example, when the snake
needs to converge onto image edges, then the external energy function needs to be
τ
1
and
∂