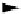Biomedical Engineering Reference
In-Depth Information
y
(
x
)
y
(
x,t
+
D
t
)
y
(
x,t
)
V
F
F
y
x
1
x
Figure 4.
Variables for propagating graph.
Plugging the speed function
F
(
κ
)=1
−
κ
and the formula
κ
=
−
ψ
xx
/
(1 +
ψ
x
)
3
/
2
into Eq. (17), we have
ψ
t
−
(1 +
ψ
x
)
1
/
2
=
ψ
xx
(1 +
ψ
x
)
3
/
2
.
(18)
Differentiating both side yields an evolution equation:
u
x
1+
u
2
]
x
,
u
t
+[
−
(1 +
u
2
)
1
/
2
]
x
=
[
(19)
where
u
=
dψ/dx
.
Comparing this curvature-modified propagating equation with Eq. (15), it is
analogous to a viscous hyperbolic conservation law. The linkage shows us that the
role of curvature in a propagating front is analogous to the role of viscosity in this
hyperbolic conservation law. It keeps the moving front smooth and differentiable
during propagation.
3.2.2. Adapting Speed Function for Image Segmentation
After examining the curvature term in the speed function, we now return to the
segmentation problem. Consider a medical image in which our goal is to isolate an
organ from the background. Starting from an initial contour, we want the moving
front to propagate inside the homogeneous region and stop at the boundaries.
Malladi, Sethian, and Vemuri [38, 39, 9] and Caselles et al. [16] [10, 40] first
proposed to use the level set methods to solve the shape recovery problem. The
propagating function is represented as
∂φ
∂t
=
g
I
(
F
A
+
F
G
)
|∇
φ
|
.
(20)