Environmental Engineering Reference
In-Depth Information
are easier to deal with than the solutions inside an empty sphere. This
y¼
0
boundary condition is still useful for the
finite barrier provided by
j
, the metallic
work function, whose measured value is 4.83 eV [30] for gold.
However, as we will see, the main parameter describing a metal is
E
F
the
Fermi
energy
, which is determined only by the density of electrons, independent of the work
function value.
The wavefunction (see Equation 2.16 in Chapter 2) is easily extended to three
dimensions:
3
=
2
sin
ðn
x
px
y ¼ð
2
=
LÞ
=
LÞ
sin
ðn
y
py
=
LÞ
sin
ðn
z
pz
=
LÞ:
ð
2
:
16a
Þ
While these were presented as bound states, they are equally valid as linear
combinations of traveling waves. This is true since sin
kx¼
(e
ikx
e
ikx
)/
i
2, and we
can consider these states to be superpositions of oppositely directed traveling waves
y
þ
¼
exp(
ikx
) and
y
¼
exp(
ikx
). Here, the moving waves,
y
, are more funda-
mental to a description of conduction processes.
We simulate a metal by adding electrons into the states de
ned by (2.16a). The
important quantum aspect of this situation is Paulis exclusion principle, such that
only one electron of specified spin can occupy a state. For a given choice of
n
x
,
n
y
, and
n
z
only two electrons, one of spinup and one spindown, can be accommodated. If we
add a large number of electrons to the box, the quantumnumbers and energies of the
successively
filled states will be given by
E
n
¼½h
2
8
m
e
L
2
ðn
x
þn
y
þn
z
Þ:
=
ð
2
:
15a
Þ
We need to know how the highest
filled energy changes as we add electrons. To
learn this, it is convenient to rewrite Equation 2.15a as
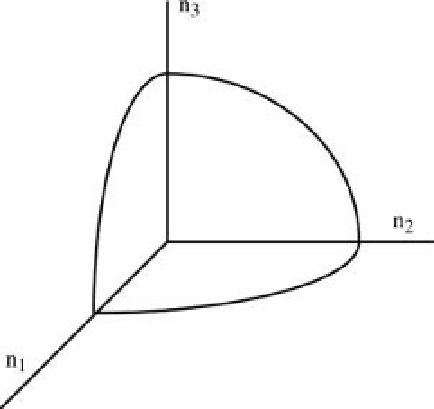
Figure 3.9 Positive octant showing spherical surface of constant energy. The number of states is
twice the volume of this octant. (Courtesy of M. Medikonda).