Information Technology Reference
In-Depth Information
x
1
1
2
w
1
1
1
y
0
w
2
0
x
2
1
2
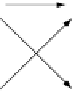
Abbildung 6.13: Radiale-Basisfunktionen-Netz mit nur zwei versteckten Neuronen,
die zwei ausgewählten Trainingsbeispielen entsprechen.
auf (man beachte die Einsen in der ersten Spalte, die der zusätzlichen festen Ein-
gabe 1 für den Biaswert entsprechen) und müssen nun für jedes Ausgabeneuron
u
einen (erweiterten) Gewichtsvektor
w
u
=(
u
,
w
uv
1
,...,
w
uv
k
)
bestimmen, so dass
A
·
w
u
=
o
u
,
o
(
l
1
)
,...,
o
(
l
m
)
wobei wieder
o
u
=
.DaaberdasGleichungssystemüberbestimmt
ist, besitzt diese Gleichung i.A. keine Lösung. Oder anders ausgedrückt: Die Ma-
trix
A
ist nicht quadratisch und daher nicht invertierbar. Man kann jedoch eine gu-
te Näherungslösung (sogenannte Minimum-Norm-Lösung) bestimmen, indem man
die sogenannte (Moore-Penrose-)
Pseudoinverse
A
+
der Matrix
A
berechnet [Albert
1972]. Die (Moore-Penrose-) Pseudoinverse einer nicht quadratischen Matrix
A
wird
berechnet als
u
u
1
A
.
Die Gewichte werden schließlich mit der Gleichung
A
+
=(
A
A
)
w
u
=
A
+
·
o
u
=(
A
A
)
1
A
·
o
u
bestimmt (vergleiche die Rechnung auf Seite 90).
Wir veranschaulichen das Vorgehen wieder anhand der Biimplikation. Aus den
Tra iningsbe i spi e l en wähl en wi r das ers te , d. h.
l
1
=(
ı
(
l
1
)
,
o
(
l
1
)
)=((
0, 0
)
,
(
1
))
,und
das letzte, d. h.
l
4
=(
ı
(
l
4
)
,
o
(
l
4
)
)=((1, 1), (1)) aus. Wir gehen also von dem teil-
weise festgelegten Radiale-Basisfunktionen-Netz aus, das in Abbildung 6.13 gezeigt
ist, und müssen nun die Gewichte
w
1
und
w
2
und den Biaswert
bestimmen. Dazu
stellen wir die 4
3Matrix
11
e
4
e
2
e
2
1
A
=
.
e
2
e
2
1
e
4
1
1
auf. Die Pseudoinverse dieser Matrix ist die Matrix
abba
cdde
eddc
A
+
=(
A
A
)
1
A
=
,
wobei
a
0.1810,
b
0.6810,
c
1.1781,
d
0.6688,
e
0.1594.