Information Technology Reference
In-Depth Information
y
6
5
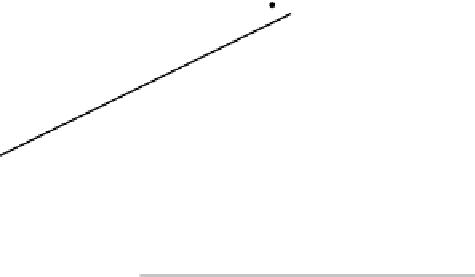
Abbildung A.3: Beispieldaten
und mit der Methode der
kleinsten Quadrate berechnete
Ausgleichsgerade.
4
3
2
1
x
0
0
12
3
4
56
7
8
x
1
2
3
4
5
6
7
8
y
1
3
2
3
4
3
5
6
Um das System der Normalgleichungen aufzustellen, berechnen wir
8
i
=
1
x
i
= 36,
8
i
=
1
x
i
= 204,
8
i
=
1
y
i
= 27,
8
i
=
1
x
i
y
i
= 146.
Damit erhalten wir das Gleichungssystem (Normalgleichungen)
8
a
+
36
b
=
27,
36
a
+
204
b
=
146,
das die Lösung
a
=
4
und
b
=
12
besitzt. Die Ausgleichsgerade ist also
3
4
+
7
12
x
.
y
=
Diese Gerade ist zusammen mit den Datenpunkten, von denen wir ausgegangen
sind, in Abbildung A.3 dargestellt.
Das gerade betrachtete Verfahren ist natürlich nicht auf die Bestimmung von Aus-
gleichsgeraden beschränkt, sondern lässt sich mindestens auf Ausgleichspolynome
erweitern. Man sucht dann nach einem Polynom
y
=
p
(
x
)=
a
0
+
a
1
x
+
...
+
a
m
x
m
mit gegebenem, festemGrad
m
,dasdie
n
Messpunkte
(
x
1
,
y
1
)
,...,
(
x
n
.
y
n
)
möglichst
gut annähert. In diesem Fall ist
n
i
=1
(
p
(
x
i
)
y
i
)
2
=
n
i
=1
(
a
0
+
a
1
x
i
+
...
+
a
m
x
i
y
i
)
2
F
(
a
0
,
a
1
,...,
a
m
)=
zu minimieren. Notwendige Bedingung für ein Minimum ist wieder, dass die parti-
ellen Ableitungen nach den Parametern
a
0
bis
a
m
verschwinden, also
F
a
0
=
0,
F
a
1
=
0,
F
a
m
=
0
. . .
,