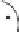Anhänge - Computational Intelligence - page 410

x 2

b = r 2
r 1

c

n =( a 1 , a 2 )

r

d
| n | n

q =

| n |

g

p

d =

pn

x 1

O

Abbildung A.1: Eine Gerade und die sie beschreibenden Größen.

verwenden. Durch Ausmultiplizieren der Normalenform sehen wir außerdem, dass
d =

pn gilt.
Die Beziehungen der Parameter der verschiedenen Gleichungsformen sind in Ab-
bildung A.1 anschaulich dargestellt. Wichtig ist vor allem der Vektor q ,derunsAuf-
schluss über die Bedeutung des Parameters d der impliziten Form gibt. Der Vektor q
wird durch Projektion des Stützvektors p auf die Normalenrichtung der Gerade be-
stimmt. Dies geschieht über das Skalarprodukt. Es ist

pn = | p || n | cos .

Aus der Zeichnung sieht man, dass |

q | = | p | cos gilt. Folglich ist

|

pn |
|

| d |
|

n | .
| d | misst also den Abstand der Gerade vom Ursprung relativ zur Länge des Norma-
lenvektors. Gilt

|

q | =

n | =

a 1 + a 2 = 1, d. h., hat der Normalenvektor n die Länge 1, so gibt | d |
direkt diesen Abstand an. Man spricht in diesem Fall von der Hesseschen Normalform
der Geradengleichung.
Berücksichtigt man noch, dass pn negativ wird, wenn n nicht (wie in der Zeich-
nung) vom Ursprung weg, sondern zum Ursprung hin zeigt, so erhält man schließ-
lich (wie auch in der Zeichnung angegeben):

d
|

q = pn
|

n | n

n
|

n | = n | .

Man beachte, dass q stets vom Ursprung zur Gerade zeigt, unabhängig davon, ob n
vomUrsprung weg oder zu ihm hin zeigt. Damit kann man aus demVorzeichen von
d die Lage des Ursprungs ablesen:

|

n |

d = 0: GeradegehtdurchdenUrsprung,
d < 0: n =( a 1 , a 2 ) zeigt vom Ursprung weg,
d > 0: n =( a 1 , a 2 ) zeigt zum Ursprung hin.
Die gleichen Berechnungen können wir natürlich nicht nur für den Stützvektor p der
Gerade, sondern für einen beliebigen Vektor x durchführen (siehe Abbildung A.2).