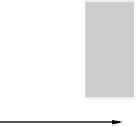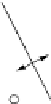Information Technology Reference
In-Depth Information
x
1
x
2
y
x
1
w
1
0
0
0
y
1
0
0
0
1
0
w
2
x
2
1
1
1
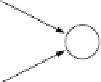
Abbildung 3.19: Ein Schwellenwertelement mit zwei Eingängen und Trainingsbei-
spiele für die Konjunktion
y
=
x
1
x
2
.
x
1
1
2
1
x
2
0
y
2
0
1
x
2
x
1
0
1
Abbildung 3.20: Geometrie des gelernten Schwellenwertelementes für
x
1
x
2
.Die
rechts gezeigte Gerade hat die Gleichung 2
x
1
+
x
2
=
3.
leicht nach, dass der Online-Lernvorgang genau dem in Abbildung 3.16 links dar-
gestellten entspricht. Analog zeigt Tabelle 3.3 den Batch-Lernvorgang. Er entspricht
dem in Abbildung 3.16 in der Mitte bzw. rechts gezeigten.
Als weiteres Beispiel betrachten wir ein Schwellenwertelement mit zwei Eingän-
gen, das so trainiert werden soll, dass es die Konjunktion seiner Eingänge berech-
net. Ein solches Schwellenwertelement ist zusammen mit den entsprechenden Trai-
ningsbeispielen in Abbildung 3.19 dargestellt. Wir beschränken uns bei diesem Bei-
spiel auf das Online-Training. Den entsprechenden Lernvorgang für die Startwerte
=
w
1
=
w
2
=
0mitLernrate1zeigtTabelle3.4.AuchhieristdasTrainingerfolg-
reich und liefert schließlich den Schwellenwert
=
3unddieGewichte
w
1
=
2und
w
2
=
1. Das gelernte Schwellenwertelement ist zusammen mit der geometrischen
Deutung seiner Berechnungen in Abbildung 3.20 dargestellt. Man beachte, dass es
tatsächlich die Konjunktion berechnet, auch wenn der Punkt (1,1) auf der Trennge-
rade liegt, da es nicht nur für die Punkte rechts der Gerade die Ausgabe 1 liefert,
sondern auch für alle Punkte auf ihr.
Nachdemwir zwei Beispiele für erfolgreiche Lernvorgänge gesehen haben, stellt
sich die Frage, ob die Algorithmen 3.2 und 3.3 immer zum Ziel führen. Wir können
zunächst feststellen, dass sie für Funktionen, die
nicht
linear separabel sind, nicht
terminieren. Dies ist in Abbildung 3.5 anhand des Online-Lernvorganges für die Bi-
implikation gezeigt. Epoche 2 und 3 sind identisch und werden sich folglich endlos
wiederholen, ohne dass eine Lösung gefunden wird. Dies ist aber auch nicht verwun-
derlich, da der Lernvorgang ja erst abgebrochen wird, wenn die Summe der Fehler
über alle Trainingsbeispiele verschwindet. Nun wissen wir aber aus Abschnitt 3.3,
dass es kein Schwellenwertelement gibt, das die Biimplikation berechnet. Folglich
kann der Fehler gar nicht verschwinden, der Algorithmus nicht terminieren.