Information Technology Reference
In-Depth Information
x
y
w
y
x
0
1
1
0
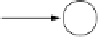
Abbildung 3.12: Ein Schwellenwertelement mit einemEingang und Trainingsbeispie-
le für die Negation.
2
2
2
e
e
e
1
1
1
2
2
2
1
1
1
Fehler für
x
=
0
Fehler für
x
=
1
Fehlersumme
Abbildung 3.13: Fehler für die Berechnung der Negation mit Schwellenwert.
Als Fehlerfunktion definieren wir zunächst, wie ja auch naheliegend, den Abso-
lutwert der Differenz zwischen gewünschter und tatsächlicher Ausgabe. Diese Feh-
lerfunktion ist in Abbildung 3.13 dargestellt. Das linke Diagramm zeigt den Fehler
für die Eingabe
x
= 0, für die eine Ausgabe von 1 gewünscht ist. Da das Schwel-
lenwertelement eine 1 berechnet, wenn
xw
,istderFehlerfüreinennegativen
Schwellenwert 0 und für einen positiven 1. (Das Gewicht hat offenbar keinen Ein-
fluss, da ja die Eingabe 0 ist.) Das mittlere Diagramm zeigt den Fehler für die Einga-
be
x
= 1, für die eine Ausgabe von 0 gewünscht ist. Hier spielen sowohl das Gewicht
als auch der Schwellenwert eine Rolle. Ist das Gewicht kleiner als der Schwellenwert,
dann ist
xw
<
,somitdieAusgabeundfolglichauchderFehler0.DasrechteDia-
gramm zeigt die Summe der beiden Einzelfehler.
Aus dem rechten Diagramm kann nun ein Mensch sehr leicht ablesen, wie das
Gewicht und der Schwellenwert gewählt werden können, so dass das Schwellen-
wertelement die Negation berechnet: Offenbar müssen diese Parameter in dem un-
ten links liegenden Dreieck der
w
-
-Ebene liegen, in demder Fehler 0 ist. Ein automa-
tisches Anpassen der Parameter ist mit dieser Fehlerfunktion aber noch nicht mög-
lich, da wir die Anschauung der gesamten Fehlerfunktion, die der Mensch ausnutzt,
im Rechner nicht nachbilden können. Vielmehr müssten wir aus dem Funktionsver-
lauf an demPunkt, der durch das aktuelle Gewicht und den aktuellen Schwellenwert
gegeben ist, die Richtungen ablesen können, in denen wir Gewicht und Schwellen-
wert verändern müssen, damit sich der Fehler verringert. Das ist aber bei dieser Feh-
lerfunktion nicht möglich, da sie aus Plateaus zusammengesetzt ist. An „fast allen“
Punkten (die „Kanten“ der Fehlerfunktion ausgenommen) bleibt der Fehler in allen
Richtungen gleich.
3
3
Der unscharfe Begriff „fast alle Punkte“ lässt sich maßtheoretisch exakt fassen: Die Menge der Punkte,
an denen sich die Fehlerfunktion ändert, ist vom Maß 0.