Noninvertible Maps and Critical Sets - Nonlinear Oligopolies: Stability and Bifurcations - page 295

asymptotic dynamics are trapped. As some parameter is varied, global bifurcations
that cause sudden qualitative changes in the properties of the attracting sets can be
detected by observing contacts of critical curves with invariant sets. The repeated
application of the inverses “repeatedly unfolds” the state space, so that a neighbor-
hood of an attractor may have preimages far from it, thus giving rise to complicated
topological structures of the basins, that may be formed by the union of several
(even infinitely many) disconnected portions. In fact, from (C.11) it follows that in
order to study the extension of a basin and the structure of its boundaries one has
to consider the properties of the inverse relation T 1 . The route to more and more
complex basin boundaries, as some parameter is varied, is characterized by global
bifurcations, also called contact bifurcations, due to contacts between the critical set
and the invariant sets that form the boundaries of the basins of attraction.

C.3 Critical Sets and the Delineation of Trapping Regions

Portions of the critical set CS and its images CS k D T k .CS/ can be used to obtain
the boundaries of trapping regions to which the asymptotic dynamics of the iterated
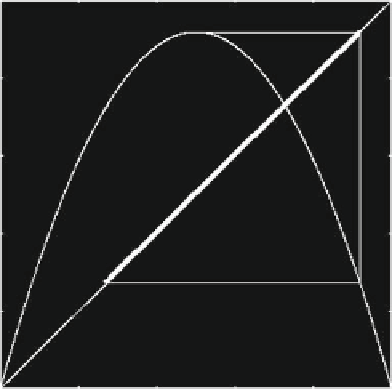
points of a noninvertible map are confined. This can be easily explained for a one-
dimensional noninvertible map, for example the quadratic map (C.1). In fact, it is
quite evident that if we iterate the logistic map for 3<<4starting from an initial
condition inside the interval Œc 1 ;c, with c 1 D f.c/, no images can be obtained
out of this interval (see Fig. C.5), that is the interval along the 45 ı line formed by
the critical point c and its rank-1 image c 1 is trapping. Moreover, any trajectory

1

c

c 1

0 1

Fig. C.5 The trapping region of the quadratic map. Trajectories starting from any point in .0;1/,
will enter the trapping region after a finite number of iterations