Chemistry Reference
In-Depth Information
by a different number of rank
1 preimages, for example Z
k
and Z
kC2
(this
is the standard occurrence for continuous maps). The critical set CS is the
n-dimensional generalization of the notion of local minimum or local maximum
of a one-dimensional map, and of the notion of
critical curve
LC of a noninvertible
two-dimensional map. This terminology, and notation, originates from the notion of
critical point as it is used in the classical works of Julia and Fatou. The set CS
1
is the generalization of local extremum point of a one-dimensional map, and of the
fold curve
LC
1
of a two-dimensional noninvertible map.
As an illustration, we consider the one-dimensional quadratic map (logistic map)
x
0
D
f.x/
D
x.1
x/:
(C.1)
This map has a unique critical point c
D
=4, which separates the real line into the
two subsets: Z
0
D
.c;
C1
/, where no inverses are defined, and Z
2
D
.
1
;c/,
whose points have two rank-1 preimages (Fig. C.1a). These preimages can be
computed by the two inverses
p
.
4x
0
/
2
:
(C.2)
If x
0
2
Z
2
, its two rank-1 preimages, computed according to (C.2), are located sym-
metrically with respect to the point c
1
D
1=2
D
f
1
.=4/
D
f
2
.=4/. Hence,
c
1
is the point where the two merging preimages of c are located. As the map (C.1)
is differentiable, at c
1
the first derivative vanishes.
We remark that in general the condition of vanishing derivative is not sufficient
to define the critical points of rank-0 since such a condition may be also satisfied by
points which are not local extrema (for example the inflection points with horizontal
tangent). Moreover, for continuous and piecewise differentiable maps the condition
of vanishing derivative is not necessary as well, because such maps may have the
property that the images of points where the map is not differentiable are critical
points, according to the definition given above. This occurs whenever such points
are local maxima or minima, like in the cases shown in Figs. C.2a, b. In Fig. C.2a,
p
.
4x
0
/
2
1
2
1
2
C
x
1
D
f
1
.x
0
/
D
D
f
2
.x
0
/
D
I
x
2
f
Z
0
f
q
−
*
f
(1)
c
1
c
f
(0)
0
x
c
x
1
f
p
*
Foldin
(b)
c
−
1
Z
2
f
−
1
2
c
−
*
1
q
Unfolding
x
c
−
x
R
R
f
−
1
1
(a)
(c)
Fig. C.1
(
a
) The preimages of the logistic map. (
b
) The folding action of the logistic map. (
c
)The
unfolding action of the inverses
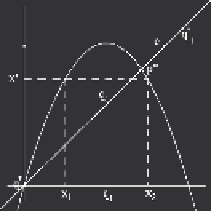

























Search WWH ::

Custom Search