Chemistry Reference
In-Depth Information
1.4
1.4
1.4
a
2
B
a
2
B
a
2
B
F
F
2
F
F
H
F
2
F
2
H
H
F
F
a
1
B
a
1
B
a
1
B
F
1
F
1
0
1.8
1.8
0
1.8
0
F
1
(a)
(b)
(c)
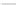
Fig. 5.6
Duopoly with heterogeneous players, the bifurcation curves with respect to the parame-
ters a
1
=B and a
2
=B,wherea
i
is the speed of adjustment of firm i and B is the slope of the demand
curve. In all cases A
0:5.The
shaded area
is the learning region, the
curve
F is the
flip boundary and H the Neimark-Hopf boundary. (
a
)Herec
2
D
D
5 and c
1
D
0:8 so that c
1
=2 < c
2
<2c
1
,
the F and H curves do not intersect and the learning region is bounded only by the flip curve. (
b
)
Now c
2
D
1:3 and the F and H curves intersect; the learning region is bounded by both curves.
(
c
)Herec
2
D
1:4 and the portion of the arc of H included in the boundary of the stability region
increases due to increasing heterogeneity
This means that, just after the loss of stability of ", the long run evolution of the
trajectories of (5.106) is characterized by the convergence to a periodic cycle
of period two. So, if firms adopt the learning process introduced above, then
they will never learn the true demand function. They will keep on underestimat-
ing/overestimating it, as the subjective scale factors continue to oscillate. If the cost
parameters c
1
and c
2
are not too different, that is in the case of moderate hetero-
geneity in costs, then according to (5.111) the steady state " can lose stability only
via a period doubling bifurcation. This is particularly true if players are identical, as
the analysis in Example 5.9 has already shown.
Let us now consider what happens if the parameters a
1
=B and a
2
=B are varied,
so that they cross the bounda
r
y of the learning region along the portion of curve H.
In this case, the equilibrium " changes from a stable focus to an unstable focus via
a supercritical Neimark-Hopf bifurcation.
3
This means that the long run evolution
of the trajectories of (5.106) converges to a quasi-periodic motion around the steady
state. Again, this implies that, on the basis of the adjustment process adopted, play-
ers will never learn the true demand function, as they will continue to over- and
underestimate prices. This kind of route to instability can only occur if the two
players are sufficiently heterogeneous with respect to cost parameters, according to
and we prefer to rely on numerical evidence as a stable 2-cycle close to the saddle " is numerically
detected whenever the parameters cross the bifurcation curve F .
3
Also in this case, a rigorous proof of the supercritical nature of the Neimark-Hopf bifurcation
requires a center manifold reduction and the evaluation of higher order derivatives, up to the
third order (see for example Guckenheimer and Holmes (1983)). This is rather tedious in a two-
dimensional m
a
p, and we prefer to rely on numerical evidence as a stable orbit surrounding the
unstable focus " is numerically detected whenever the parameters cross the bifurcation curve H.










Search WWH ::

Custom Search