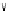Database Reference
In-Depth Information
(
G
,
1)
(
G
,
2)
(
G
,
1)
(
G
,
2)
(
L
,
1)
(
L
,
2)
(
L
,
1)
(
L
,
2)
(b)
(a)
Figure 5.1 Dependency graphs of (a)
{
θ
1
}
and (b)
{
θ
1
,
θ
2
}
.
Look at the example in
Figure 5.1
(for now, ignore the
annotation of some of the
edges). The graph in the left part of the figure corresponds to
θ
1
, and it has no cycles;
the graph in the right part of the figure corresponds to
, and it has a cycle. So
intuitively, the notion of acyclicity does the job prohibiting nonterminating chase.
We will see that the chase will terminate, and do so in polynomiallymany steps, if the set
of target tgds is acyclic. But in fact we will do more. The notion of acyclicity could be too
restrictive sometimes (although it does arise in several examples; for instance we shall see
it again when we deal with XML data exchange by means of relational representations).
If we look at the definition of the simple dependency graph, we see that there are two
kinds of edges, and only the second kind, to an existentially quantified variable, actually
creates a new value in the target instance. So it seems that all we need to do is to forbid
cycles involving such value-creating edges, and this will be enough to rule out infinite
chase sequences.
We now modify the definition of a graph of a set of tgds. If Σ is a set of tgds over R
t
, its
dependency graph
has the same nodes as before, and two kinds of edges: usual ones, and
edges with a special label
. For every tgd
{
θ
1
,
θ
2
}
∀
x
∀
y
(
ϕ
(
x
,
y
)
→∃
z
ψ
(
x
,
z
)) in
Σ
, and for every
variable
x
mentioned in
x
that occurs in the
i
th position of relation
R
in
, we add an edge
from (
R
,
i
) to (
T
,
j
) if the variable that occurs in the
j
th position of relation
T
in
ϕ
ψ
is:
•
x
itself, or
•
an existentially quantified variable
z
; in this case, the edge from (
R
,
i
) to (
T
,
j
) that we
add is labeled
.
Definition 5.9 (Weak acyclicity) A set
Σ
of tgds is
weakly acyclic
if the dependency
graph of
Σ
does not have a cycle going through an edge labeled
.
Example 5.10 (
Example 5.4
continued) Returning to
Figure 5.1
, we see that it depicts
dependency graphs of
{
θ
1
}
(which is weakly acyclic), and
{
θ
1
,
θ
2
}
(which is not).
Of course every acyclic set of tgds is weakly acyclic too, as the edges in the dependency