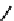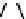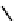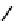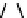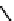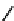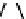Database Reference
In-Depth Information
•
all trees in them are labeled by some fixed alphabet, and
•
nodes with the same label have tuples of attributes of the same length.
These assumptions can be easily avoided but we use them for now as they keep the notation
simple.
A natural analog of naıve tables are trees with (reused) variables. In this role they
are simply pure child-only patterns using constants and reusing variables We shall write
Π
p
(C
ONST
,
↓
,
=) for such patterns. They are the same ones as those in
(14.1)
but without
the
//
.
Thus, for XML trees, the notions of models and theories are defined as follows. For a
set of patterns
B
,wehave
π
case. They will serve the role of the language
L
Mod(
B
)=
{
T
|
T
|
=
π
for every
π
∈
B
.
T
T
For a set
of XML trees we define its theory Th(
) as
Th(
T
)=
{
π
∈
Π
p
(C
ONST
,
↓
,
=)
|
T
|
=
π
for all
T
∈T }
.
This theory provides the certain knowledge (in the language
Π
p
(C
ONST
,
↓
,
=)) that can
be extracted from
T
. Max-descriptions are then the closest we can get to defining
T
in
Π
p
(C
ONST
,
↓
,
=).
Definition 14.4 Let
T
be a set of XML trees. A pattern
π
∈
Π
p
(C
ONST
,
↓
,
=) is a
max-
T
description
of
if
Mod(
π
)=Mod(Th(
T
))
.
We now illustrate the notion of max-descriptions by revisiting the example shown in
Figure 14.3
. A max-description for them is obtained by merging all the trees in part (d)
of that figure at the root. We also asked about a modification of the example where the
a
-nodes carry data values, as shown in
Figure 14.4
. Then a max-description of
{
T
1
,
T
2
,
T
3
}
is the tree in part (d) of the figure. It has three occurrences of variables and preserves the
certain knowledge about the grandchildren of the root.
r
r
r
r
a
(1)
a
(2)
a
(1)
a
(2)
a
(1)
a
(2)
a
(
x
)
a
(
y
)
a
(
z
)
c
c
c
c
b
d
b
d
d
b
b
d
(a)
T
1
(b)
T
2
(c)
T
3
(d) a max-description
Figure 14.4 Why max-descriptions work
Now that we understand the notion of a proper representation of certain information
contained in a set of trees, we apply this notion to answering XML queries that can produce
trees. Suppose we have a query
Q
that takes trees as inputs and returns trees. Our goal is
to define certain answers to such a query over a set
T
of trees. We define such certain
answers as max-descriptions of the set
Q
(
T
)=
{
Q
(
T
)
|
T
∈T }
.