Advanced Topics in Inverse Imaging - Introduction to Imaging from Scattered Fields - page 184

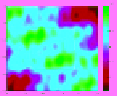
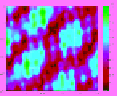
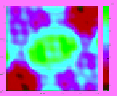
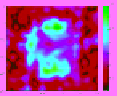
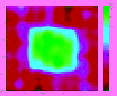
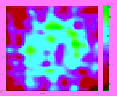
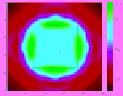
table 11.3 Family of Reconstructed Images for a Square
with Side Lengths of 2λ for Varying Permittivity Values
and Varying Number of Randomly Spaced Data Points in
k -Space (Square with Sides = 2 λ )
ε r = 1.1; N = 4.2 ε r = 1.5; N = 4.9 ε r = 1.9; N = 5.5

NN/2

8 12 18

NN

16 30 36

2NN

32 48 72

4NN

72 108 144

12,960

12,960

12,960

is, of predicting the scattered field from a known scattering object can be dif-
ficult We have focused here primarily on the scattering of electromagnetic
waves and provided an overview of those interactions and, we hope, a histori-
cal perspective on how concepts and models have developed over the years.
The most tractable modeling approach is clearly to linearize the problem. More
precisely, assuming both linearity and time or space invariance of these gov-
erning models allows elegant Fourier-based techniques to be applied. We cite,
for example, the huge literature on Fourier optics, a subset of physical optics,
and the widely used first Born approximation. A Fourier relationship between
a scattering function and the measured field allows a wealth of methods for
image recovery and enhancement to be brought to bear on the problem. We
have discussed how to address the limited data problem, resolution enhance-
ment, and phase information retrieval based on this underlying model.
In practice, scattering is rarely sufficiently weak or involves such a suffi-
ciently slowly varying scattering parameter (Rytov approximation) for these
weakly scattering models to apply. Much effort has gone into trying to better
understand the consequences of using them when they are not strictly valid,