Applications to Real Measured Data - Introduction to Imaging from Scattered Fields - page 141

“foam” of relative permittivity ε r ≈ 1.45 and inside the “foam” there is another
circular dielectric of relative permittivity ε r ≈ 3.0. From Chapter 5, Table 5.1
shows the reconstruction from the inverse Fourier transform of scattered
field data, that is, first Born reconstruction of FoamDielInt. The Born recon-
struction is computed at 6 GHz operating frequency for which the scatter-
ing strength of the object is | kVa | ≈ 22. The object represents a fairly strong
scatterer, | kVa | ≫ 1, as a result of which we see that the first Born recon-
struction is not all that good. For FoamDielInt and FoamDielExt, the emitting
antenna was placed at eight different locations which were 45° apart whereas,
for FoamTwinDiel and FoamMetExt, which are more complicated objects, the
emitting antenna was positioned at 18 locations with 20° angular intervals.
The receiving antenna collected complex data at 1° intervals. The scattering
experiment was conducted using nine operating frequencies, which range
from 2 GHz to 10 GHz.
The number of degrees of freedom for one of these objects is approximately
given by 11 × 11 cm 2 × 1.8/λ 2 , and the wavelength varies from 15 cm to 3 cm
depending on the frequency used. This gives 1 < N < 25 assuming no metal is
included. However, it is the highest frequency case that will dictate whether
the number of measurements taken is sufficient At lower frequencies, the
data collection might well be adequate but the resolution limit using 2 GHz
illumination is approximately the size of the entire scattering object, revealing
only whether it is there or not; not very useful in our opinion. If we consider
N = 25, then 4 N 2 = 2500. Assuming 18 antenna positions and measurements of
the scattered field for each and every degree, the total number of data avail-
able are 6300. This should be sufficient for the nonmetallic objects. For the
choice of only eight incident field directions, 2800 is just about sufficient
Consequently, we would argue that we can have some confidence in algo-
rithms that recover good reconstructions from the Institut Fresnel data of the
sets of nonmetallic objects.
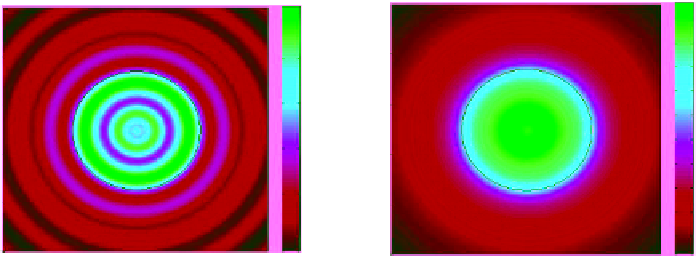
Finally, in Section 6.4, we discussed imaging resonant objects and noted
the improved appearance of the reconstruction of cylinders when illuminated
at frequencies close to their Mie resonant frequencies. Figure 9.26 shows on
the left a reconstruction of a cylinder with large permittivity, the black circle

(a) (b)

×10 -0

0 0

0.03

12

11
10
9
8
7
6
5
4
3

50 50

0.025

100 0.02 100

0.015

150 150

0.01

200 200

0.005

250 0 250 0

50 100 150 200 250 50 00 150 00 250

Figure 9.26 (a) An image of a cylinder with large permittivity making the first Born approximation invalid.
(b) More uniform reconstruction of the cross section of a cylinder for a weaker scatterer with ε r = 1.1. The left side
image, as expected, has approximately the correct diameter.