Applications to Real Measured Data - Introduction to Imaging from Scattered Fields - page 125

(a) (b)

10
9
8
7
6
5
4
3
2

80

60
40
20

0

-20
-40
-60
-80
-80 -60 -40-20 0 0 0 0 0

mm

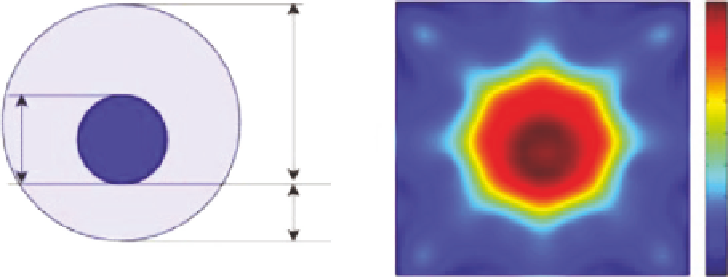
Figure 9.10

FoamDielInt: (a) Actual object, (b) Born reconstruction.

FoamDielInt at 6 GHz. Figure 9.11 shows the implementation of the method to
estimate the FoamDielInt object. The available data was made causal by mov-
ing it into one quadrant, and then a reference point was added such that the
phase of V Ψ lies between +π and −π.
A Gaussian filter was then applied to the cepstral domain, and was then
reduced in diameter until no discernable wave-like features associated with
Ψ remained in the final image, which is obtained as a further inverse Fourier
transform of the filtered cepstrum and exponentiation. Figure 9.11e shows
the reconstruction obtained by applying cepstral filtering The ratio of the
contrast of the reconstructed cylinders matches the ratio of the permittivi-
ties in the original object. Figure 9.11c shows a log-plot of the cepstrum of
V Ψ after the reference point has been added. The log-plot is used to view the
low energy features in the cepstral domain. The success of cepstral filtering
relies on V Ψ being minimum phase, which is dependent upon the amplitude
and location of the “artificial” reference point. Figure 9.12 shows the varia-
tion in the quality of reconstruction as we change the reference point ampli-
tude. Figure 9.12c shows that the quality of reconstruction improves as we
get closer to satisfying the minimum phase condition. FoamDielInt was also
computed for various other frequencies; the results are shown in Figure 9.13.
One of several factors that will affect the quality of the reconstruction (apart
from the difficulties associated with inverting multiply scattered data) is the
data determined image point-spread function. Figure 9.14 shows the point
spread function for different frequencies calculated from the inverse Fourier
transformation of the set of delta functions which mark the locations of the
sampling points in k -space, as provided by Institut Fresnel. These indicate the
extent of features that one can hope to resolve in the final reconstructions of the
scattering object V ( r ) from the measured scattered data in an ideal situation.
At lower frequencies, that is, 3 GHz, the locus of data in k -space is over a
much smaller radius Ewald circle than for the 10 GHz case. As a consequence,
the main lobe of the point-spread function is much larger at lower frequen-
cies of illumination, and therefore, one can expect to see a lower resolution
reconstruction. However, low frequency illumination also implies a better
image estimate of V ( r ) based on the conditions for the validity of the first Born
approximation, since a condition for the Born approximation to be valid is