Homomorphic (Cepstral) Filtering - Introduction to Imaging from Scattered Fields - page 111

u

H ( u, υ )

H ( u, ν )

(a) (b) (c)

1.0

0.9

250

0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1

0.9

D 0 = 10
D 0 = 20
D 0 = 40
D 0 = 100

0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1

200
150
100
50

0.8
0.6
0.4
0.2

0.667

50 100 150 200 250

50 100 150 200 250

ν

D ( u, υ )

50 100 150 200 250

u

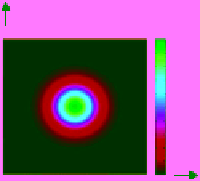
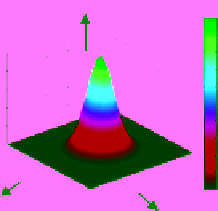
Figure 8.4 Gaussian low pass filter. (a) Gaussian low pass filter 2-D view, (b) Gaussian low pass filter dis-
played in 3-D, and (c) cross section of Gaussian low pass filter.

In addition, for the Gaussian filter, the profile is shown for various values of
sigma, which in effect defines the filter bandwidth.
As is commonly known in basic filter theory (Jackson, 1991), and verified
in Shahid (2009), the performance of the Gaussian is generally better than the
ideal filter since the ideal filter is prone to produce “ringing” in the recon-
structed image as illustrated in Figure 8.5. This being the case, the Gaussian
filter is the preferred filtering process in the cepstrum domain. This still
leaves the question as to what are the optimum values for the parameters for
this filter, More specifically, what should the value of sigma be for the filter,
which governs the bandwidth of the filter, and what are the constraints and
effects for the peak value of the filter? These parameters will be examined in
detail in the following section.

8.6 ReMovIng the ReFeRenCe
One final technique that will be demonstrated in this chapter pertaining to
filtering or attenuating the Ψ term is that of subtracting a cepstrum version
of illuminating incident wave Ψ 0 in the cepstrum domain in an attempt to
improve the reconstructed image, or possibly improve the scale of the recon-
structed image. If we review for a moment the final version of the V Ψ product,
which strictly corresponds to V Ψ/Ψ inc , obtained in Equation (8.16), we have
that this product can be approximated as

V
RR

‚ + 〈〉

Ψ

� -

≈ log

′

As stated earlier it is evident that there is a “noise” term in this expres-
sion that appears to be of the form of a “weighted” incident frequency type
term, depending on how strong a scatterer the target is. This being the case,
it seems that it would be beneficial to take the incident field and obtain a
weighted cepstrum representation of it and subtract it from the expression
above. Assuming that the correct weighting factor is found, it appears that
this would have some positive benefit to the resulting cepstrum representa-
tion of V ( r ). Moreover, there will be some benefit to trying to eliminate or
account for the reference “ R” term as well that was inserted to satisfy Rouche's
theorem. This obviously should have some effect on the overall scaling of the