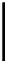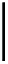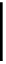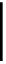Hardware Reference
In-Depth Information
Figure 4.63: MMF expressed in electric degree
Figure 4.63 shows one electrical cycle of the MMF waveform. We can use
this waveform for the Fourier analysis of the MMF waveform in the entire
motor airgap. This waveform can also be used to analyze the distribution of
airgap
fi
eld as they are similar, according to the analysis given in section 4.2.1.
The result of the Fourier analysis of the MMF generated by one phase
winding in the 9-slot motor is presented in Table 4.2. The spectrum of the
airgap MMF is shown in Figure 4.64.
Table 4.2: MMF Harmonics produced by the one phase winding in the 9-slot
spindle motor with normal winding format
Order of Harmonic
1
2
4
5
6
7
√
3
π
√
3
2π
√
3
4π
√
√
√
3
5π
3
7π
3
8π
Harmonic Value
The results presented in Table 4.2 and Figure 4.64 show that the airgap
fi
eld generated by the concentrated winding is rich in harmonics. According
to the conditions for torque generation introduced earlier in section 4.2.8, the
pole-pair of the magnet installed on the rotor determines the motor pole-pair,
and it must match one of the harmonic
fi
elds generated by the airgap MMF. It
is logical to select the fundamental harmonic of the MMF to match the motor
pole-pair as it is the strongest among all the harmonics of the airgap
fi
elds.
The pole-pair of the fundamental harmonic is equal to the cycle number of the
winding on the stator core. Therefore, for a spindle motor with 9 slots, the
magnetic ring can be made with 3 pole-pairs. In a similar way, the number of
motor pole-pairs can be obtained for spindle motor with different numbers of
stator slots. For examples, if there are 6 stator slots, then the 3-phase winding
can form 2 cycles, and the motor pole-pair should be chosen as 2. If the number
of slots is 12, the winding cycle is 4, and the motor pole-pair can be 4.