Hardware Reference
In-Depth Information
2
0
1.8
0.04
1.6
0.16
1.4
0.36
0.64
1.2
1
0.8
0.6
0.4
0.2
0
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Time (secs)
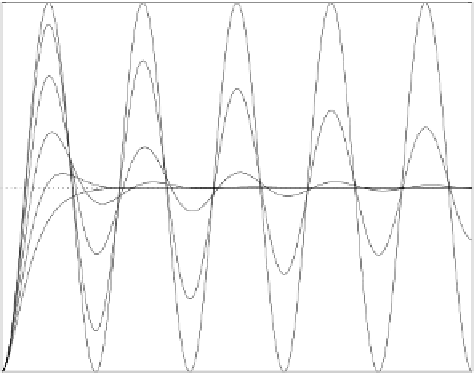
Figure 3.7: Step response of a second order model for different damping ratios.
depends on the value of the corresponding damping ratio. Smaller the damp-
ing ratio, longer it takes for the resonance to be diminished. The step re-
sponses of the second order plant of equation 3.16 are shown in Figure 3.7
for different damping ratios. This figure shows responses for ω
n
=2π with
ζ
n
=0, 0.04, 0.14, 0.36, 0.64 and 1.0. As can be seen here, if the damping ratio
is low, for example ζ
n
≤ 0.1 which is typical of a mechanical resonance, the
step response is highly oscillatory.
If the controller is designed using a rigid body model of the plant ignor-
ing the resonances, the response of the closed loop system shows oscillations
whenever there is a change in reference command. Though these oscillations
may eventually decay to zero, the performance of the servomechanism is ham-
pered as it takes longer time for settling. Designing controller using rigid body
model also ignores the gain and phase changes caused by the resonant mode
dynamics, which may have more severe consequences on the stability. Effects
of resonant modes can be minimized by adding a filter between the controller
and the plant. Either a low pass filter or a notch filter can be used for this
purpose. However, notch filter is prefered over low pass filter because of the
cut-off in the magnitude response is sharper for notch filter and notch filter
introduces lower phase in the loop. A simple notch filter that can be used to
cancel the resonant frequency ω
n1
is described by the transfer function
F(s)=
s
2
+2ζ
n1
ω
n1
s +ω
n1
s
2
+2ζ
n2
ω
n2
s +ω
n2
,
(3.17)
whose numerator cancels the lightly damped poles of the plant model (3.5).
The denominator of the filter transfer function can be the stable numerators