Information Technology Reference
In-Depth Information
g1(x)
1
0.8
0.6
0.4
-4
-2
0.2
0
x1
0
-4
2
-2
0
2
4
4
x2
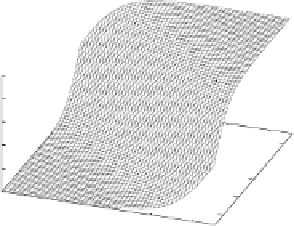
Fig. 4.2.
Plot of the softmax function
g
1
(
x
) by (4.5) with inputs
x
=(1
,x
1
,x
2
)
T
,and
gating parameters
v
1
=(0
,
0
,
1),
v
2
=(0
,
1
,
0)
[71, 121]. It begins with the observation that maximisation of the likelihood is
simplified if the values of the latent variables were known, as in (4.3). Hence,
assuming that
Z
is part of the data,
D
=
{
X
,
Y
}
is referred to as the
incomplete
data
,and
is known as the
complete data
. The EM-algorithm
proceeds with the expectation step, by finding the expectation of the complete
data log-likelihood
D∪{
Z
}
=
{
X
,
Y
,
Z
}
E
Z
(
l
(
θ
;
D∪{
Z
}
)) with the current model parameters
θ
fi-
xed, where
l
(
θ
;
X
,
θ
) is the logarithm of the joint density
of the outputs and the values of the latent variables. In the maximisation step
the above expectation is maximised with respect to the model parameters. When
iterating this procedure, the incomplete data log-likelihood
l
(
θ
;
D∪{
Z
}
)
≡
ln
p
(
Y
,
Z
|
) is guaranteed
to increase monotonically until a maximum is reached [174]. More details on the
application of the EM-algorithm to train the MoE model are given by Jordan
and Jacobs [121]. We will now consider each step in turn.
D
The Expectation Step
Using (4.7), the complete-data log-likelihood is given by
l
(
θ
;
D∪{
}
≡
ln
p
(
Y
,
Z
|
X
,
θ
)
Z
)
N
=ln
p
(
y
n
,
z
n
|
x
n
,
θ
)
n
=1
N
K
=
z
nk
(ln
g
k
(
x
n
)+ln
p
(
y
n
|
x
n
,
θ
k
))
(4.10)
n
=1
k
=1
where
θ
is the set of expert parameters
and gating parameters
V
.
When fixing these parameters, the latent variables are the only random variables
in the likelihood, and hence its expectation is
{
θ
1
,...,
θ
K
}
N
K
E
Z
(
l
(
θ
;
D∪{
Z
}
)) =
r
nk
(ln
g
k
(
x
n
)+ln
p
(
y
n
|
x
n
,
θ
k
))
,
(4.11)
n
=1
k
=1









Search WWH ::

Custom Search