Database Reference
In-Depth Information
≈
FIGURE 5.1
: PARAFAC provides a three-way decomposition with some
similarity to the singular value decomposition.
notations but are equivalent:
r
x
ijkl
≈
A
it
B
jt
C
kt
D
lt
,
t
=1
r
X
≈
A
t
◦
B
t
◦
C
t
◦
D
t
,
(5.1)
t
=1
X
(
m×npq
)
B
)
T
.
≈
A
(
D
C
Without loss of generality, we typically normalize all columns of the factor
matrices to have unit length and store the accumulated weight (i.e., like a
singular value) in a vector
λ
:
r
X
≈
λ
t
(
A
t
◦
B
t
◦
C
t
◦
D
t
)
.
t
=1
It is common practice to order the final solution so that
λ
1
≥ λ
2
≥···≥λ
r
.
In the discussion that follows, we describe a general algorithm for a four-way
model without
λ
because this normalization can be performed in a post-
processing step.
Our goal is to find the best fitting matrices
A, B, C,
and
D
in the minimiza-
tion problem:
X
−
2
r
min
A,B,C,D
A
t
◦
B
t
◦
C
t
◦
D
t
.
(5.2)
t
=1
The factor matrices are not required to be orthogonal and, in fact, are usu-
ally not in most practical applications. Under mild conditions, PARAFAC
provides a unique solution that is invariant to factor rotation (19).
Given a value
r>
0 (loosely corresponding to the number of distinct
topics or conversations in our data), PARAFAC finds matrices
A
m×r
,
∈
R
n×r
,
C
p×r
,and
D
q×r
B
∈
R
∈
R
∈
R
to yield Equation (5.1). Each group
{
,for
j
=1
,...,r
, defines scores for a set of terms, authors,
recipients, and time for a particular conversation in our email collection; the
value
λ
r
after normalization defines the weight of the conversation. (Without
loss of generality, we assume the columns of our matrices are normalized to
A
j
,B
j
,C
j
,D
j
}














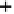




















Search WWH ::

Custom Search