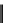Information Technology Reference
In-Depth Information
Figure 10.16.
A labeled numeric game tree
1
move 1
move 2
Max can guarantee
a value of 1.
-1
1
8
-1
9
1
2
3
5
-5
8
7
-1
-2
9
1
-12
-10
2
3
(worse for Min) than the state beside it (with a value of 7). In other words, if Max had
to choose, he should choose to move to the leftmost state.
Applying the minimax procedure to this truncated tree results in a label for every
node, as shown in figure 10.16. Max's best move here according to all the estimates is
move 2, where he will be guaranteed a value of 1 or better no matter what Min does.
But why not simply truncate the tree at depth 1 and use the estimates from there
instead of going to depth 3? The answer is that the estimates are expected to be more
accurate
, the closer the depth is to the end of the game. An estimate at level 1 may be
much less useful than the values obtained by minimax with estimates at deeper levels.
So there is a trade-off: the deeper the search using estimates, the more accurate the
results will be, but the more nodes have to be considered to decide on a best move. In
fact, as with planning (see section 9.3), the number of nodes to be considered grows
exponentially
with the depth of the tree.
∗
A version of minimax in Prolog
There are many ways to encode the minimax procedure in Prolog, but the easiest is
to assume a number
v
and find a move (if one exists) that guarantees a value of
v
or better (that is, bigger for Max and smaller for Min). The property to be used in a
program is that Max can guarantee a value of
v
or higher if he can move to a state
where Min
cannot
guarantee a value of
v
1 or lower. Similarly, Min can guarantee a
value of
v
or lower if she can move to a state where Max
cannot
guarantee a value of
v
−
+
1
or higher.