Java Reference
In-Depth Information
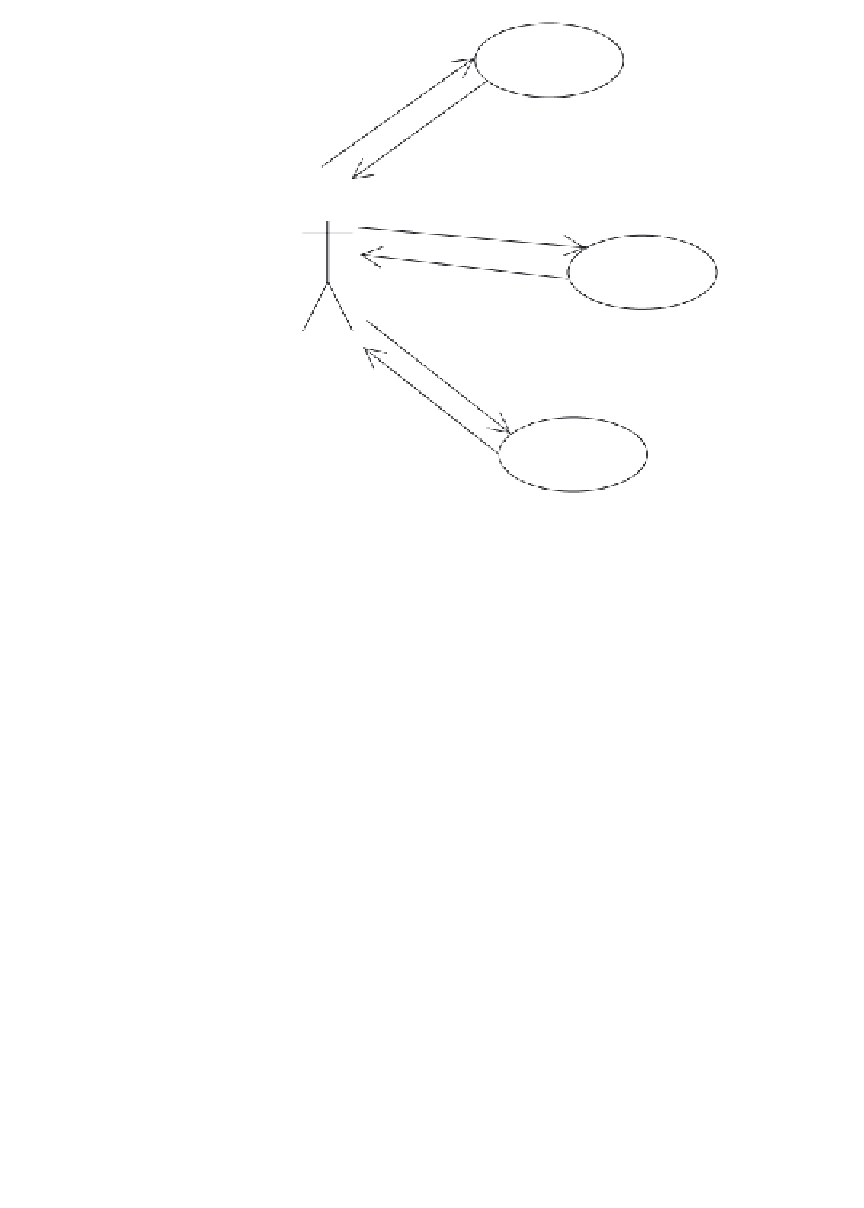
Calculation
Change format
User
Change base
Figure 6.1
Calculator use cases
are well known and have a coded mathematical foundation. A summary of
these concepts is presented below.
Number bases
Currently in most cultures people learn mathematics using the decimal
base, but several other bases are possible. For instance, computer science
utilizes the binary base.
The number base defines how many different digits can be used to repre-
sent a number. Table 6.2 shows a summary of the most important bases. For
instance, the binary base uses two symbols: “0” and “1”. For the hexadeci-
mal base, since the decimal digits are not sufficient, by convention the
letters of the alphabet are used; so “A” stands for 10, “B” for 11 and so on.
We are considering the
positional
representation of numbers, i.e. the
value represented by a digit depends not only on the digit itself but also on
its position inside the number.
A positional representation system, whose base is B, is represented as
follows:
c
n
...
c
2
c
1
c
0
.
c
−
1
c
−
2
...
c
−
m
Table 6.2
Bases and digits
Name
Base
Digits
binary
2
0, 1
decimal
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
hexadecimal
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F