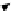Information Technology Reference
In-Depth Information
(
s
)=
s
s
be the set of interactive transitions that leave
s
,and
α
−−→
-
IT
λ
⇒
s
}
-
MT
(
s
)=
{
s
be the set of Markovian transitions that leave
s
.
A state
s
is
Markovian
iff
MT
(
s
)
=
∅
and
IT
(
s
)=
∅
;itis
interactive
iff
MT
(
s
)=
∅
and
IT
(
s
)
=
∅
.Further,
s
is a
hybrid state
iff
MT
(
s
)
=
∅
and
IT
(
s
)
=
∅
; finally,
s
is a
deadlock state
iff
MT
(
s
)=
IT
(
s
)=
∅
.Let
MS ⊆
S
and
IS ⊆
S
denote the
sets of Markovian and interactive states in IMC
.
A labeled transition system (LTS) is an IMC with
I
MT
(
s
)=
∅
for any state
s
. A continuous-time Markov chain (CTMC) is an IMC with
IT
(
s
)=
∅
for any
state
s
.(Thecaseinwhich
(
s
) for any
s
is both an LTS and a
CTMC). IMCs are thus natural extensions of labeled transition systems, as well
as of continuous-time Markov chains.
MT
(
s
)=
∅
=
IT
The semantics of an IMC.
Roughly speaking, the interpretation of Markovian
transition
s
λ
⇒
s
is that the IMC can switch from state
s
to
s
within
d
time
units with probability 1
e
−λ·d
.Thepositiverealvalue
λ
thus uniquely identifies
a negative exponential distribution. For a Markovian state
s
−
,let
R
(
s, s
)=
∈ MS
{
λ
⇒
be the
rate
to move from state
s
to state
s
.If
R
(
s, s
)
>
0for
more than one state
s
, a competition between the transitions of
s
exists, known
as the
race condition
. The probability to move from such state
s
to a particular
state
s
within
d
time units, i.e., the Markovian transition
s
s
}
λ
|
s
s
wins the race,
→
is given by:
e
−E
(
s
)
·d
,
where
E
(
s
)=
s
∈S
R
(
s, s
) denotes the
exit rate
of state
s
.Intuitively,it
states that after a delay of at most
d
time units (second term), the IMC moves
probabilistically to a direct successor state
s
with discrete branching probability
P
(
s, s
)=
R
(
s,s
)
E
(
s
)
1
R
(
s, s
)
E
(
s
)
·
−
.
α
s
0
s
3
0
.
6
0
.
2
s
1
0
.
3
0
.
1
0
.
4
0
.
4
α
s
2
s
4
β
Fig. 1.
Example of an IMC with Markovian and interactive states
Example 1.
Consider the IMC
of Fig. 1 where dotted arrows denote interactive
transitions and solid arrows Markovian transitions. We have
I
MS
=
{
s
0
,s
1
,s
4
}
and
IS
=
{
s
2
,s
3
}
. Markovian states behave like CTMC states, e.g., the transition
0
.
3
⇒
e
−
0
.
3
·z
.The
two Markovian transitions of
s
0
compete for execution and the transition whose
s
0
s
2
expires within
z
∈
R
≥
0
time units with probability 1
−