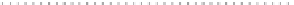Database Reference
In-Depth Information
20 (0.25)
40 (0.125)
70 (0.0625)
30 (0.0625)
15 (0.375)
25 (0.09375)
35 (0.1875) 65 (0.09375)
10 (0.375)
20 (0.09375)
30 (0.1875) 60 (0.09375)
20 (0.5)
10 (0.25)
50 (0.25)
Distribution of
w
DE
given
w
BD
=20
Fig. 8.1
The weight constrained region of
P
1
=
A
,
B
,
D
,
E
when
w
BD
takes sample 20.
8.1 Probability Calculation
There are two orthogonal issues in answering a path query
Q
l
(
,
)
: the
l
-weight
probability calculation and the path search. In this section, we first discuss how
to compute the exact
l
-weight probabilities for paths. Then, two approximate al-
gorithms are presented. We also present a straightforward depth-first path search
method. An efficient best-first path search algorithm will be introduced in Sec-
tion 8.2.
u
v
8.1.1 Exact l-Weight Probability Calculation
How can we calculate the
l
-weight probability of a path
P
when the edge weights
are correlated? We can partition
P
into subpaths such that they are conditionally
independent, as illustrated in the following example.
Example 8.1 (l-weight constrained region). Let l
=
55
and
τ =
0
.
5
. Consider path
query Q
l
(
A
,
E
)
and path P
=
A
,
B
,
D
,
E
in the probabilistic graph in Figure 2.6.
. The joint prob-
abilities f
e
1
,
e
3
and f
e
3
,
e
6
are given in Figures 2.6(c) and 2.6(d), respectively, which
specify the correlation between edges. Weights w
e
1
and w
e
6
are conditionally inde-
pendent given w
e
3
.
The conditional probability of w
e
1
given w
e
3
=
P contains three edges e
1
=(
A
,
B
)
,e
3
=(
B
,
D
)
and e
6
=(
D
,
E
)
20
is
0
.
375
,
x
=
10
or x
=
15
;
f
e
1
,
e
3
(
x
,
20
)
f
e
1
|
e
3
(
x
|
20
)=
)
=
f
e
3
(
20
0
.
25
,
x
=
20
.
The conditional probability of w
e
6
given w
e
3
=
20
is
0
.
25
,
x
=
10
or x
=
50
;
f
e
6
,
e
3
(
x
,
20
)
f
e
6
|
e
3
(
x
|
20
)=
)
=
f
e
3
(
20
0
.
5
,
x
=
20
.
The probability that w
P
is at most l when w
e
3
=
20
is