Civil Engineering Reference
In-Depth Information
use the current state or other time-variant factors to influence the outcome. When
considering a first-order chain this defines the Markov condition that: the next state
is solely dependent on the current state, or
PX
k
þ
f ¼
PX
k
þ
1
¼
j
j
X
k
¼
i
f
g ¼
p
i
;
j
ð
2
Þ
The values X
k
from the countable set S are called states. If the model param-
eters are constant over time, the MC is denominated time-homogeneous Markov
chain or stationary Markov chain. That is, the model transition matrix is a constant
time-invariant matrix independent of the time instant k
0
@
1
A
;
p
i
;
j
0
;
8
i
;
j
2
S
^
X
j
2
S
p
1
;
1
...
p
1
;
n
.
.
.
P
¼
.
.
p
i
;
j
¼
1
8
i
2
S
ð
3
Þ
p
m
;
1
... p
m
;
n
This mathematical model describes a system that undergoes transitions between
states with a certain probability. Likewise, there exists a probability of observing a
space in a state and an additional probability of switching from that state (Fig.
5
).
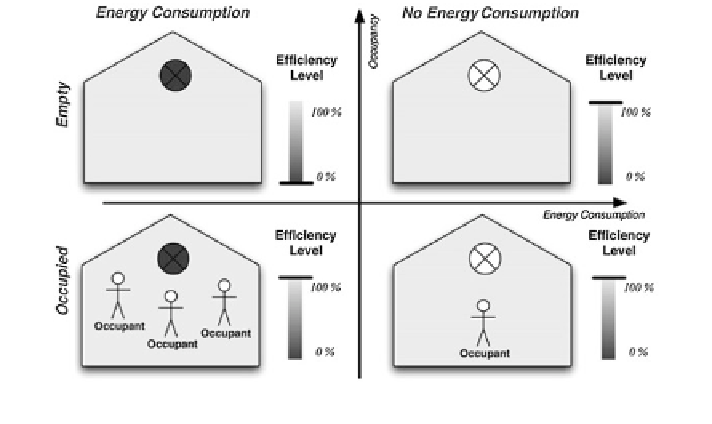
If considering that the spaces' states are based on the observations over time,
the spaces are modelled using a state-space approach. A possible state decom-
position is illustrated in Fig.
6
. The spaces can either be occupied or empty, and
the lighting system can either be turned on or off. The result is a discrete state
space with four states S
¼
S
0
;
S
1
;
S
2
;
S
3
which represent: empty space with energy
consumption; empty space with no energy consumption; occupied space with
energy consumption and occupied space with no energy consumption, respectively.
The stochastic nature is related to the transitions between these states.
Fig. 5
Graphical interpretation of 4 possible states regarding the lighting system for a space