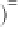Seismoelectric theory in partially saturated conditions - The Seismoelectric Method - page 81

Equation (3.76) yields the following Hooke ' s law for the is given by

effective stress given by

J T = J + J d 3 85

u T T + p a I + α w p w − p a I = λ ∇ u I + G ∇ u + ∇ 3 78

E + k ∗ ω Q V
η w

2

J T = σ ∗ ω ∇ p w − ω ρ w s w u − i ωε E 3 86

u T T eff = λ ∇ u I + G ∇ u + ∇ 3 79

Equation (3.86) can be written as an equation in which
we have a generalized Ohm

where the effective stress is given by Equation (3.67).
Note that the effective stress is only related to the
deformation of the skeleton of the porous material by
definition.

s law appearing on the right-
hand side of the equation together with an electrokinetic
coupling term:

'

E + k ∗ ω

Q V

σ ∗ ω −

2

J T = i ωε ∇ p w − ω ρ w s w u 3 87

3.1.3 Maxwell equations in unsaturated
conditions
Pride (1994) volume averaged the local Maxwell equa-
tions to obtain a set of macroscopic Maxwell equations
in the thin double layer limit (i.e., assuming that the
thickness of the diffuse layer is much smaller than the
size of the throat controlling the flow of the pore water).
The same equations were obtained by Revil and Linde
(2006) for the thick double layer case. The general form
of these macroscopic Maxwell equations is

η w

An effective conductivity can be introduced, such as
σ eff = ωε eff is the effective

or apparent complex conductivity and

σ ∗ ω − i ωε , where σ eff = σ eff + i

ε eff are real
scalars that are dependent upon frequency. These effec-
tive parameters are those that are measured during
an experiment in the laboratory or in the field, but
these terms contain both electromigration and true die-
lectric polarization effects. They are given by

σ eff and

σ eff = σ

and ε eff = σ ω − ε .

∇ × E = − B 3 80

∇ × H = J + D 3 81

3.2 Extension to two-phase flow

∇ B =0, B = ∇ × A 3 82

Q V

3.2.1 Generalization of the Biot theory in
two-phase flow conditions
For the generalization of the Biot

∇ D = ϕ 3 83

Frenkel theory in two-
phase flow conditions, we consider, in the following, an
isotropic porous elastic body wherein two Newtonian
fluid phases fill the full of the pore space of the solid
matrix. In this development, wave propagation through
a porous medium containing two immiscible fluids, in
the space

-

where B is the magnetic induction vector, H is the mag-
netic field (in Am − 1 ), D is the current displacement vec-
tor (in Cm − 2 ), A is the magnetic potential vector, and
E = denotes the electrostatic potential

(in V). These equations are completed by two electro-
magnetic constitutive equations: D =

−∇ ψ − A where ψ

ε E and B = μ H

time domain, is governed by coupled partial
differential equations. Here, Lo et al. (2005) presented
a formulation that used the continuum mechanics of
mixtures theory (Lo et al., 2002). This theory was derived
in an Eulerian framework and describes the propagation
of three (compressional) P-waves and one S -wave
(shear). These waves have dissipation terms that result
from the momentum transfer or interaction terms of
the solid and fluids within the porous medium. Using
numerical simulations, Santos et al. (1990, 2006) con-
cluded that both of the compressional waves are analogs
to the Biot fast and slowP-waves in a single-fluid-saturated

-

where denotes

its magnetic permeability. In the absence of magnetized
grains,

ε is the permittivity of the material and μ

μ = μ 0 where μ 0 denotes the magnetic permeabil-

ity of free space.
When the harmonic electrical field is written as

E = E 0 exp is the angular frequency with

E 0 being a constant electrical field magnitude and direc-
tion, the displacement current density vector is given by
J d = D =

− i ω t , and ω

− i ωε E . The total current density, J T , entering

Ampère ' s law,

∇ × H = J T 3 84