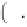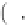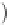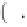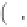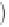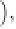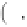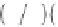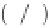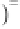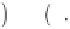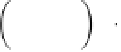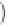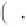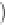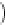Seismoelectric theory in partially saturated conditions - The Seismoelectric Method - page 80

2

ρ w k ∗ ω
i

∇ T + F = − ω ρ u + ρ f w 3 61 2

θ ω = s w α − ω 3 71

ωη w

where T is the total stress tensor (positive normal stress
implies tension; see Detournay & Cheng, 1993) and F
denotes the total body force applied to the porous mate-
rial. In unsaturated conditions, Newton

The last fundamental constitutive equation needed to
complete the hydromechanical model in unsaturated
conditions is a relationship between the total stress tensor
(or the effective stress tensor) and the displacement of
the solid phase and filtration displacement of the pore
water phase. This equation is Hooke

' s law is written as

2

∇ T + F = − ω ρ u + s w ρ w w w 3 62

s law, which, in lin-
ear poroelasticity and for saturated conditions, is given by
(Biot, 1962a,b)

'

where the filtration displacement of the pore water phase
is given by

w w = k ∗ ω
i

u T

T = λ u ∇

∇ ∇

u + ∇

2

u + C w I + G 3 72

ωη w ∇

p w − ω

ρ w s w u −

F w 3 63

u T denotes the deformation
tensor, G = G fr denotes the shear modulus that is equal
to the shear modulus of the skeleton (frame), and
λ u = K u −

where ε =12 ∇ u + ∇

Combining Equations (3.62) and (3.63) yields

ρ w k ∗ ω
i

2 2

∇ T + F = − ω ρ u + s w

ωη w ∇

p w − ω ρ w s w u − F w 2 3 G denotes the Lamé modulus in undrained

conditions ( K u denotes the undrained bulk modulus). In
unsaturated conditions and accounting for the air pres-
sure, Equation (3.70) can be written as

3 64

ρ w k ∗ ω
i

2 S

ω

2

∇ T + F = − ω ρ u − ω s w

ωη w ∇

p w − F w 3 65

u T T + p a I = λ u ∇ u + C ∇ w w I + G ∇ u + ∇ 3 73

where

ρ w 2 k ∗ ω
i

From Equation (3.45), the linearized increment of
fluid content is given by

S
ω

2

ρ = ρ − s w

ωη w ω

3 66

The effective stress in unsaturated conditions is taken as

w w = 1 p a + C −∇

M p w − M ∇

u 3 74

T eff = T + p a I + s e α p w − p a I 3 67

Combining Equations (3.73) and (3.74) yields

which is consistent with the Bishop effective stress prin-
ciple in unsaturated conditions and the Biot stress princi-
ple in saturated conditions. The confining pressure and
the effective confining pressure are defined as

2
3 G

1
M p w −

K u −

∇ −

p a − α w ∇ T + p a I = u + C u

u T

I + G ∇ u + ∇ 3 75

1
3 Trace T

2
3 G

P = − 3 68

K u − α w C

− ∇ − α w p w −

T + p a I = u p a

1
3 Trace T eff

u T P eff = − 3 69 I + G ∇ u + ∇ 3 76

where the following expression, derived previously,
has been used for the Biot coefficient in unsaturated
conditions:

−

p a − s e α p w − respectively. This yields P eff = P p a . Equa-

tions (3.65) and (3.67) yield

k ∗ ω
i

C
M = α w = s e α

2 s w ρ w 2 S

ω

∇ T eff + F − ω

ωη w F w =

− ω ρ u + θ ω ∇ p w 3 70

3 77

where the hydromechanical coupling term, θ ω ,s In addition, the bulk modulus is given by K = K u − α

w C

defined by and the Lamé modulus is given by λ = K − 2 3 G .