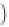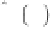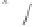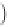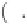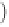Geoscience Reference
In-Depth Information
Therefore, Equations (3.36) and (3.37) provide a sim-
ple streaming potential and electroosmosis model for
porous media. This simple model can be used to charac-
terize the occurrence of the streaming potential and
electroosmosis in porous media systems.
C
0
s
w
1
C
p
ω
,
s
w
≈
3 31
−
i
ωτ
k
k
r
k
0
Q
V
C
0
= lim
ω
0
C
p
ω
,
s
w
≈
3 32
1
F
s
w
n
η
w
s
w
σ
f
+
σ
S
Similarly, the generalized electroosmotic coupling
coefficient is defined in the quasistatic limit of the
Maxwell equations. This definition is facilitated by the
following constraints: we allow for the change of the pore
fluid pressure while the skeleton is at rest with an
absence of pore fluid flow influenced by other mechan-
isms. With these constraints, the electroosmotic coupling
coefficient can then be simply defined by the ratio
between the gradient of pore fluid pressure divided by
the gradient in electrical potential. For the thin double
layer case, this yields
3.1.2 Description of the
hydromechanical model
The development of the unsaturated hydromechanical
model starts with the following Biot constitutive equa-
tion in saturated conditions:
−
p
=
C
s
∇
u
+
M
s
∇
w
3 38
Equation (3.38) is also often written as
−
p
=
C
s
ε
kk
−
M
s
ζ
3 39
,
s
w
=
∂
p
w
∂
φ
w
=0
;
u
=0
L
∗
ω
,
s
w
η
w
k
∗
ω
C
os
ω
=
−
3 33
,
s
w
where
V V
(where
V
denotes the represen-
tative elementary volume) represents the volumetric
strain
ε
kk
=
∇
u
=
δ
Q
V
ω
C
os
ω
,
s
w
=
−
3 34
of
the
porous
body
and
ζ
=
−∇
w=
Q
0
C
os
ω
V
s
−
w
,
s
w
≈ −
1
−
i
ωτ
k
3 35
ϕ
∇
u
w
denotes the linearized increment of fluid
content (e.g., Lo et al., 2002). The parameter
u
−∇
represents
the fractional volume of water flowing in or out of the
representative volume of the skeleton in response to an
applied stress. The bulk moduli,
M
s
and
C
s
, in saturated
conditions, are defined as
ζ
For the thick double layer case, the electroosmotic cou-
pling coefficient is given by
C
os
ω
≈ −
Q
0
V
s
w
. Therefore,
the electroosmotic coupling coefficient is simply a meas-
ure of the excess of charges that can be moved by the flow
of the pore water caused by an electric field. In unsatu-
rated flow conditions, it is customary to use the capillary
head gradient
1
C
s
≡−
d
ε
Δ
K
f
+
K
S
Δ
1+
kk
dp
w
=
3 40
p
w
ρ
w
g instead of the pore water
pressure gradient. Below the relaxation frequency separ-
ating the low-frequency viscous laminar flow regime
from the high-frequency inertial laminar flow regime,
Equation (3.26) can be rewritten in the time domain using
the pressure head, including the gravitational field in the
hydraulic driving force. This yields two coupled equations:
∇Ψ
=
∇
ζ
1
M
s
≡
ζ
dp
w
d
1+
Δ
=
ϕ
3 41
K
f
ε
kk
where
α
≡
1
−
K
fr
K
S
denotes the Biot coefficient
in
the
saturated
state
and
Δ
is
defined
by
K
S
Δ
K
fr
. The Biot modulus,
M
, corre-
sponds to the inverse of the poroelastic component of the
specific storage and is defined as the increase of the
amount of fluid (per unit volume of rock) as a result of
a unit increase of pore pressure under constant volum-
etric strain. From that, the following relationship is
obtained:
C
s
=
=
K
f
ϕ
1
−
ϕ
K
S
−
σ
∗
L
∗
s
w
J
w
w
∇
ψ
ρ
w
g
=
−
k
r
s
w
k
0
η
w
∇ Ψ
+
z
+
ρ
w
s
w
u
L
∗
s
w
3 36
M
s
.
To extend these equations to the unsaturated case,
we apply the classical change of variables discussed
previously,
α
where the quasistatic approximation coupling coefficient
L
∗
is given by
L
∗
s
w
=
k
r
s
w
k
0
Q
0
that
is,
ρ
f
s
w
ρ
w
,
p
p
w
,
ϕ
s
w
ϕ
, and
V
3 37
η
w
s
w
w w
w
=
s
w
ϕ
u
w
−
u
). This yields