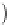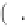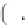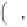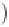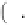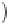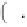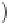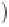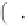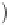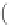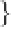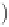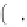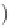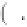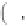Geoscience Reference
In-Depth Information
where
θ
ω
is a volumetric hydromechanical coupling coef-
ficient. Equation (2.201) corresponds to Newton
2
w
=
k
ω
∇
p
−
ω
ρ
f
u
,
2 192
s law for
a poroelastic body. This equation is similar to the classical
Newton
'
where
k
ω
is defined by
'
s law for an elastic solid except the coupling term
1
θ
ω
∇
p
, which accounts for the dynamic coupling between
the pore fluid and the solid phases.
Regarding the filtration displacement, we obtain the
following relationship between
w
and
u
and
p
:
k
ω
=
2 193
2
ω
ρ
f
+ i
ω
b
Equation (2.192) can be used in Newton
'
s law to give
2
s
ω
2
−
ω
ρ
u
−
ω
ρ
f
k
ω
∇
p
=
∇
T
,
2 194
1
M
p
2
+
S
+
∇
k
ω
∇
p
−
ω
ρ
f
+
α
u
=0
2 203
s
ω
=
ρ
+
ω
2
2
f
k
ω
,
ρ
ρ
2 195
Equation (2.203) is the classical diffusion equation for
thepore fluidpressurewitha source termrelated tothehar-
monic changeof displacementof the solidphase. Thisyields
where
ρ
s
ω
is an apparent mass density for the solid phase.
Equation (2.194) is a partial differential equation
between
u
and
p
but the stress tensor
T
also depends
on
w
. Using the relationships between stress and strain,
we obtain the following relationship between the diver-
gence of the filtration displacement,
∇
2
s
ω
−
ω
ρ
u
+
θ
ω
∇
p
=
∇
T
,
2 204
w
, and the diver-
gence of the displacement of the solid phase,
∇
1
M
p + S
+
∇
k
ω
∇
p
−
ω
2
ρ
f
+
α
u
=0 2 205
u
:
1
M
p
Therefore, in summary, the equations of motion can be
written in terms of the two new unknown fields (
u
,
p
)as
∇
w
=
−
+
S
−
α
∇
u
,
2 196
where
α
is the classical Biot coefficient of poroelasticity.
We use Equation (2.196) in the stress/strain relationships
to remove the dependence of the stress tensor on
w
. This
yields
2
s
ω
−
ω
ρ
u
+
θ
ω
∇
p
=
∇
T
+
F
,
2 206
u
T
T
=
λ
∇
u I
+
G
∇
u
+
∇
,
2 207
T
=
T
−
α
p
I
,
2 208
u
T
T
=
λ
∇
u I
+
G
∇
u
+
∇
−
α
p
I
,
2 197
1
M
p
2
+
S
+
∇
k
ω
∇
p
−
ω
ρ
f
+
α
u
=0 2 209
2
3
G
,
λ
=
K
−
2 198
s law applied
to the solid skeleton of the porous material. This equation
is similar to Newton
Equation (2.206) corresponds to Newton
'
where
is the Lamé modulus of the skeleton. The effec-
tive stress tensor is written as
λ
'
s equation of elastic bodies except for
the coupling term,
p
, which represents the coupling
between the solid and fluid phases. The stress tensor
defined by Equation (2.207) corresponds to the stress
tensor with the porous material in vacuum (i.e., it corre-
sponds to the stress acting on the solid phase if the pore
fluid is replaced by vacuum). Equation (2.208) describes
the relationship between the total stress tensor and the
effective stress tensor. The material properties entering
into Equations (2.206)
θ
ω
∇
u
T
T
=
λ
∇
u I
+
G
∇
u
+
∇
,
2 199
−
α
T
=
T
p
I
2 200
The effective stress tensor is the equivalent stress ten-
sor of the skeleton without fluid (in vacuo). Using
Equations (2.195)
(2.198) and (2.192), we obtain an
equation connecting the solid displacement and the fluid
pressure assuming that the Biot coefficient is constant:
-
-
(2.209) are given by
1
k
ω
=
ρ
f
+ i
ω
b
,
2 210
ω
2
2
s
ω
−
ω
ρ
u
+
θ
ω
∇
p
=
∇
T
,
2 201
2
3
G
,
λ
=
K
−
2 211
2
k
ω
,
θ
ω
=
α
+
ρ
f
ω
2 202