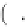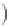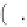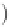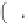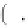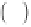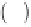Geoscience Reference
In-Depth Information
p
f
M
+
μ
=
μ
0
,
2 134
∇
w
+
α
∇
u
s
=0,
2 139
where
F
is the electrical formation factor defined in
Chapter 1 for
where
M
is one of the Biot moduli and
bt
=
η
f
t k
0
the electrical
conductivity and by
where
as
defined by Equation (2.16).Equation(2.66)isderived
from Equation (2.39) neglecting the electroosmotic effect,
and
η
f
t
is the inverse Fourier transform of
η
f
ω
Equation (2.41);
ε
s
are the dielectric constants of
the pore fluid and the solid, respectively; and
ε
f
and
μ
0
is the
magnetic permeability of free space. Note that only two
textural properties,
ρ
f
F
.
Equation (2.138) follows from Equation (2.124), while
Equation (2.139) has been derived in Section 2.1.3.1
(see Eq. 2.92) using the relationship
ρ
f
denotes the effective fluid density given by
ρ
f
=
and
F
, are required to describe
the influence of the topology of the pore network upon
the material properties entering into the transport and
EM constitutive equations.
The coupling between the mechanical and the
Maxwell equations occurs in the current density, which
can be written in the time domain as
Λ
=
C
/
M
.
Next, we take the time derivative of Equation (2.139)
and apply Darcy
α
s law in which we have neglected the
electroosmotic contribution. This method is used because
we are only interested in describing the seismoelectric
coupling and not electroseismic effects in this topic. The
assumption of whether the electroosmotic component
can be neglected in this type of EM
'
J
=
σ
E
+
J
S
,
2 135
Q
0
V
hydromechanical cou-
pling formulation process has been investigated by Revil
et al. (1999b). From this formulation process, we obtain,
in the frequency domain, the following hydraulic diffusion
equation for the pore water:
-
k
ω
J
S
=
Q
0
V
w
=
−
∇
p
f
+
ρ
f
u
s
−
F
f
,
2 136
η
f
where
J
S
(in Am
-
2
) is the source current density of elec-
trokinetic nature. The body force
F
f
can be responsible for
EM signals that are directly associated with the source
(see discussions in Chapter 5). An important point is that
we expect a resonance effect in the source current
density, and due to the resonance effects in the Darcy
velocity, as shown in Figure 2.1 for a capillary. Such
resonances associated with harmonic resonance due to
bulk flow have never been observed to date.
−
i
ω
p
f
k
ω
η
f
2
+
∇
−∇
p
f
+
ω
ρ
f
u
s
=
α
∇
i
ω
u
s
2 140
M
The first term in Equation (2.140) corresponds to the
storage term, while the second term corresponds to the
divergence of the Darcy velocity. The term on the right-
hand side of Equation (2.140) corresponds to a source
term for this partial differential equation.
Combining Equations (2.137) and (2.138) yields
2.1.5 Analysis of the wave modes
In this section, we solve the seismoelectric model for a
poroelastic media saturated by Newtonian or generalized
viscoelastic fluids. Specifically, the case of a poroelastic
body saturated by a Newtonian fluid is a special case of
the theory developed previously. In the following text,
we develop the general field equations, and in the proc-
ess, we show that these equations yield estimates that are
consistent with the classical Biot
ρ
−
ρ
f
F
1
F
∇
T
f
+
bt
F
u
s
=
∇
T
−
w
,
2 141
−
ρ
f
ρ
T
f
−
ρ
f
bt
F
F
ρ
f
w
=
∇
ρ
∇
T
−
w
2 142
The dissipation mechanism occurring in our model
stems from the viscoelastic properties of the pore fluid.
In the time domain, the constitutive equations for the
total stress tensor and the fluid phase average stress ten-
sor have been derived in Section 2.1.3.4 and are shown in
Equations (2.143) and (2.144):
Frenkel theory in the
limit of a Newtonian fluid at low frequencies.
The three equations to solve are given, in the time
domain, by Darcy
-
s law plus the combined equations of
motion for the solid and the fluid phases:
'
bt
w
+
ρ
f
w
=
− ∇
p
f
+
ρ
f
u
s
−
F
f
,
2 137
T
=
K
U
∇
u
s
I
+
C
∇
w I
+2
G
U
t
d
s
2 143
ρ
u
s
+
ρ
f
w
−∇
T
=
F
,
2 138
+2
C
G
t
d
w
,