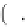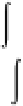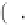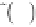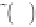Geoscience Reference
In-Depth Information
F
=
1
1
1
1
−
2
i
ω ω
c
,
e
2
dV
p
,
ω
=
2 41
c
2 45
V
V
p
and
c
0
=
ε
f
ζ η
f
σ
f
(Helmholtz
-
Smoluchowski equation;
see von Smoluchowski, 1906) where
ζ
is the so-called
zeta potential (the inner potential of the electrical diffuse
layer; see Chapter 1).
Using the dynamic viscosity defined by Equation (2.16)
and using Equation (2.45), the dynamic relative coupling
coefficient of a porous material saturated by a generalized
Maxwell fluid in the thin double layer assumption is
given by
e
2
dV
p
=2
V
p
Λ
,
2 42
e
2
dS
S
where
dV
p
denotes an integration over the pore space and
dS
denotes an integration over the pore
-
solid interface.
The normalized electrical field
e
=
is obtained by
solving the following canonical Laplace problem for an
average disk in the direction of the macroscopic electrical
field (see Pride, 1994):
∇Γ
m
c
1
−
i
ωτ
Γ
has units of length and satisfies
c
ω
=
2 46
m
c
1
−
2
i
ω ω
c
1
−
i
ωτ
2
the Laplace equation
∇
Γ
= 0 throughout the pore space
with boundary conditions
Γ
=0on
z
=0 and
Γ
=
L
on
z
=
L
and
n
= 0 on both the internal interface between the
solid and fluid phases (
n
is the unit vector at the solid
∇Γ
In Equation (2.46), the effect of the viscosity appears
twice: in the numerator because of the dependence of
C
0
with the viscosity and in the last term in the denom-
inator because of the dependence of the critical fre-
quency
-
fluid interface pointing inside the solid) and on the exter-
nal surface of the averaging disk (
n
is the outward unit
vector). This approach assumed implicitly the continuity
of the solid phase at the scale of a representative elemen-
tary volume of the porous rock. Note that Pride did not
use the formation factor in his model but instead he
defined the bulk tortuosity of the pore space, which
is
ω
c
with the viscosity. It is interesting to see that
Equation (2.46) has the same asymptotic limit at low fre-
quencies as Equations (2.40) and (2.44) corresponding
to a thick electrical double layer (using the Donnan
assumption). This limit is given by 1 +
i
ω ω
for a
c
.
The dynamic streaming potential coupling coefficient
is given by
α
∞
=
F
ϕ
Newtonian fluid.
The excitation of the pore fluid in the resonance fre-
quency band of the viscoelastic fluid yields an amplifica-
tion of the value of the streaming potential coupling
coefficient by several orders of magnitude with respect
to the value of
Q
V
k
ω
η
f
σ
C
ω
=
−
2 43
the streaming potential coupling
coefficient at
low frequencies. We expect
that
the
The normalized coupling coefficient is given by
determination of
c
ω
in a wide range of frequencies
(e.g., 0.01
10 kHz in the laboratory) could help to char-
acterize the properties of the oil contained in the pores
through the determination of both
-
C
C
0
c
ω
≡
=
k
ω
2 44
τ
m
, the peak of the
relaxation time, and
, which characterizes the broadness
of the distribution of relaxation times associated with the
composition of the oil in terms of polymers.
With the basis established earlier in this section, we can
determine, within an order of magnitude, the DC value
of the streaming potential coupling coefficient of a
sandstone filled with a polar oil. For the Berea sandstone
(permeability ~10
−
13
m
2
, porosity ~0.18), an analysis of
the data displayed by Alkafeef et al
.
(2006) for the
streaming current density versus the fluid pressure gradi-
ent yields
Q
V
=10
−
4
Cm
−
3
. Alkafeef et al. (2006) used a
α
Therefore, in our approach, the normalized dynamic
coupling coefficient is equal to the normalized dynamic
permeability, the normalization being made with respect
to the low-frequency values of these parameters
k
0
and
C
0
.
Using the thin double layer assumption (small size of
the diffuse layer with respect to the size of the pores),
the dynamic relative coupling coefficient of a porous
material saturated by a viscous Newtonian fluid is given
by (Pride, 1994)