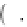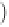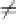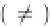Introduction to the basic concepts - The Seismoelectric Method - page 31

EP , p = E 1 P − p ,0 + E 2 P = p , p 1 126

δ ij = 0f i j
1f i = j

1 133

Equation (1.124) can be written in terms of bulk defor-
mation as and G denotes the shear modulus of the material, which

is equal to the shear modulus of the skeleton (as long as
the fluids do not sustain shear stresses). The two first
terms of the right-hand side of Equation (1.132) corre-
spond to the classical Hooke

ε kk P , p = ε kk P − p ,0 + ε kk P = p , p 1 127

1
K P

1
K S p

s law in elastic media, and
the last term corresponds to the effect of the pore fluid
pressure. We are going to demonstrate that this equation
is consistent with the effective pressure law determined
in Section 1.5.1.
Taking thenondiagonal components of Equation (1.132)
yields

'

ε kk P , p = − − −

p 1 128

The bulk deformation can be written in terms of an
effective pressure P ∗ as

1
K P ∗

ε kk P , p = − 1 129

T ij i j =2 G ε ij 1 134

P ∗ = P − α p 1 130

which corresponds to pure shear. We look now for
Hooke

K
K S

α =1 − 1 131 ' s law for the bulk deformation. We have

T kk ≡ Tr T 1 135

is called the effective stress coefficient
or Biot coefficient. Equation (1.129) means that from the
standpoint of the bulk deformation, having a confining
pressure P and an internal pore fluid pressure p is equiv-
alent of having a confining pressure P ∗ and no fluid pres-
sure. We can proceed now to a complete analysis of the
Biot coefficient

The coefficient α

T kk ≡ 3 K ε kk − α p 1 136

where Tr( ) denotes the trace of thematrix corresponding
to the tensor (sum of the diagonal elements). The confin-
ing pressure is related to the bulk stress by

0. If
K S K (for instance, at high porosity, the compressibility
of the skeleton is high), we have

α . We have K S ≥ K and therefore α ≥

1
3 T kk =

P ≡ − − K ε − α p 1 137 kk

= 1. In this last case, the
effective pressure is equal to the differential pressure
P

α

and therefore, we can check the property

p . This situation is known as the Terzaghi effective
stress principle (Terzaghi, 1943) and was developed ini-
tially for porous soils. In the case where the porosity is
equal to zero, we have K = K S , and therefore,

-

1
K P

1
K P ∗

ε kk = − − α p = − 1 138

= 0, which
is consistent with the idea that at very low porosity (e.g.,
for crystalline rocks), the fluid pressure will play no role.
A typical value of the Biot coefficient for a sandstone
is 0.8.

α

which is consistent with Equation (1.129).

1.5.3 Drained versus undrained regimes
In the drained regime, the fluid is free to move in and out
of a representative elementary volume that is undergoing
deformation, and doing so, it dissipates energy. The fluid
pressure can be considered as constant, and the mass of
fluid per unit volume of rock is variable. In the undrained
regime, the fluid cannot (or has no time to) move in/out
with respect to the representative elementary volume. In
this case, the fluid resists to the deformation. The drained
and the undrained bulk moduli are defined by

1.5.2 Hooke ' s law in poroelastic media
In a linear poroelastic material, the constitutive Hooke ' s
law is written as

2
3 G

T ij = K − ε kk δ ij +2 G ε ij − α p δ ij 1 132

where δ ij is the Kronecker delta defined by