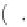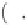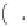Geoscience Reference
In-Depth Information
be estimated (e.g., from core samples), depth profiles of
either porosity or selected fluid properties could be
derived using Equation (7.7). This could be of interest
where porosity estimates are not available or, for exam-
ple, fluid properties change significantly at depth such as
at contaminated land sites.
The longer-period seismoelectric conversion compo-
nents (Figures 7.6a and 7.8) are most likely manifesta-
tions of the direct field, as documented previously by
Kulessa et al. (2006). These components are most likely
caused by transient streaming potentials generated by
ground compression owing to the impact of the hammer
on a poorly cemented top sandstone layer. This could
generate transient water movement toward the two
dipoles and act effectively as the superposition of a series
of electrical dipoles to produce the direct field.
where the superscript
These
three equations correspond to (i) a macroscopic momen-
tum conservation equation for the solid phase, (ii) a con-
stitutive equation for the effective stress tensor,
T
, and
(iii) a momentum conservation equation for the pore
fluid. In these equations,
I
is the identity matrix,
u
repre-
sents the averaged solid displacement vector (in m),
w
denotes the averaged fluid
“
T
”
denotes
“
Transpose.
”
solid relative displacement
vector (in m),
M
symbolizes one of the Biot coefficients
(described in the following text), and
p
is the average
fluid pressure in the pore water phase. The relationship
between the effective stress tensor,
T
, and total stress
tensor,
T
(in Pa), is
-
T
=
T
−
α
p
I
7 13
The Biot coefficients
M
and
α
are given by (Revil &
Mahardika, 2013; see Chapter 3)
7.3 Numerical modeling
1
M
=
1+
Δ
K
f
θ
,
7 14
In this section, we present a numerical experiment that
simulates the field study discussed earlier. The goal of this
exercise is not to reproduce exactly the field seismoelec-
tric data, but to place the inferred empirical model, relat-
ing seismoelectric conversions to volumetric water
contents, on a solid physical grounding. We begin with
a summary of the relevant theory developed in Revil
andMahardika (2013) by first describing the propagation
of seismic waves in poroelastic media before providing
the equations that govern electrokinetic processes in
unsaturated conditions, accounting for variability of fluid
saturation.
α
=1
−
K K
S
,
7 15
where
represents the volumetric water content
(dimensionless, equal to the porosity at saturation),
Δ
θ
=
s
w
ϕ
K
fr
, and
K
s
and
K
f
are the bulk
moduli of the solid and fluid phases, respectively. Two
mechanical properties enter into these equations:
=
K
f
ϕ
K
S
1
−
ϕ
K
S
−
λ
is
the drained Lamé coefficient
(in Pa) defined by
λ
2 3
G
where
K
=
K
fr
and
G
=
G
fr
symbolize the
bulk modulus and the shear modulus of the solid frame
(index
=
K
−
solid skeleton without any fluid inside),
respectively. The density,
“
fr
,
”
, in Equation (7.10) repre-
sents an apparent mass density of the solid phase. The
coupling term in Equation (7.1),
ρ
S
ω
7.3.1 Theory
Assuming an
e
−
j
ω
t
time dependence for the mechanical
disturbances (
j
being the pure imaginary number,
j
2
=
θ
ω
, denotes a hydrome-
chanical coupling coefficient,
k
ω
and (
k
ω
(inm
6
s
2
kg
−
1
)in
Equation (7.12) is a permeability-related constant. These
three coefficients are given by (see Jardani et al., 2010,
and Chapter 2)
−
1,
ω
is the angular frequency, and
t
is time) while using
the displacement of the solid phase and the pore pressure
as unknowns instead of the solid and fluid phase dis-
placement vectors,
the poroelastodynamic equations
of motion,
in the frequency domain, are given by
1
k
ω
=
b
,
7 16
(Chapter 2)
ω
2
ρ
f
+
i
ω
2
S
ω
S
ω
2
f
k
ω
,
−
ω
ρ
u
+
θ
ω
∇
p
=
∇
T
,
7 10
ρ
=
ρ
−
ω
ρ
7 17
u
T
T
=
λ
∇
u I
+
G
∇
u
+
∇
,
7 11
2
θ
ω
=
α
−
ω
ρ
f
k
ω
,
7 18
p
M
+
∇
2
k
ω
∇
−
ω
ρ
f
u
=
−
α
∇
p
u
,
7 12
ρ
f
=
F
ρ
f
,
7 19