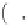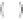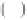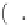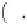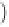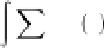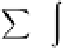Geoscience Reference
In-Depth Information
smooth. The activity or concentrations of the ions in
the electrical diffuse layer are determined through the
use of Poisson
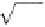
In the general case, the charge density in the diffuse layer
is given by
Boltzmann statistics. To understand these
distributions, we need to define the so-called electro-
chemical potentials of cations (+) and anions (
-
∞
N
Q
S
=
q
i
C
i
χ
d
χ
1 16
). These
electrochemical potentials are defined by (e.g., Gouy,
1910; Hunter, 1981)
-
i
=1
0
∞
N
q
i
φχ
k
b
T
C
i
exp
Q
S
=
q
i
−
d
χ
1 17
i
=1
0
i
+
k
b
T
ln
α
i
+
q
i
φ
μ
i
=
μ
1 11
0
We have also the useful property (Pride, 1994)
where
±
is the chemical potential of the ions in a ref-
erence state (a constant),
k
b
is the Boltzmann constant,
T
is temperature (in degrees K, Kelvin),
μ
0
∞
q
i
φχ
k
b
T
q
i
φ
d
2
k
b
T
α
i
is the activity of
species i (equal to the concentrations for dilute solutions),
q
i
is the charge of species i (in C; for instance,
q
(+)
=
e
for
Na
+
where
e
denotes the elementary charge 1.6 × 10
−
19
C),
and
exp
−
d
χ
=2
χ
d
exp
−
1 18
0
where 2
χ
d
represents an average thickness for the diffuse
is the electrostatic potential (in volts, V).
Local thermodynamic equilibrium between the electri-
cal diffuse layer and the bulk pore water is given by the
equality of the electrochemical potentials. We can con-
sider equilibrium between a position
φ
ε
f
k
b
T
2
e
2
C
f
1 2
where
e
denotes the elemen-
tary charge 1.6 × 10
−
19
C,
k
b
denotes the Boltzmann con-
stant, and
layer (
χ
d
=
ε
f
denotes the dielectric constant of water). The
length scale
χ
d
is called the Debye screening length in
electrical double layer theory (e.g., Gouy, 1910,Chapman,
1913). From Equations (1.17) and (1.18), we obtain
away from the
OHP (see position in Figure 1.1) and an arbitrary position
in the bulk pore water for which the local potential of the
electrical diffuse layer
χ
=0 . For mono-
valent ions, the condition (Hunter, 1981)
φ
vanishes
φ
∞
N
q
i
C
i
X
q
i
Q
S
=2
χ
d
1 19
i
=1
μ
i
χ
=
μ
i
∞
1 12
The potential in the diffuse layer is approximately given
by the Debye formula
φχ
=
φ
d
exp
−
χ χ
d
(e.g., Pride,
1994) where
φ
d
denotes the local potential on the
OHP. For a binary symmetric 1:1 electrolyte, the expres-
sion of the charge density of the diffuse layer reduces to
(using Eq. 1.15)
yields
0
i
+
k
b
T
ln
0
i
+
k
b
T
ln
f
i
μ
α
χ
±
e
φχ
=
μ
α
1 13
i
In Equation (1.13),
α
f
±
denotes the activity of the
cations (+) or anions (
-
) far from the mineral surface
and taken in the bulk pore water (in the bulk pore fluid,
characterized by superscript f). It follows that the ionic
activity of species i at the position of the OHP itself,
α
Q
S
=
aC
f
sinh
−
φ
d
2
k
b
T
1 20
a
=8×10
3
ε
f
k
b
TN
1 21
i
, is given as a function of the activity in the bulk pore
water
α
i
by
where
N
denotes the Avogadro number (6.0221 × 10
23
mol
−
1
). We can rewrite the charge density of the diffuse
layer as
i
=
i
X
2
q
i
α
α
1 14
φ
d
2
k
b
T
Q
S
=
1
2
1
X
X
= exp
−
1 15
aC
f
X
−
1 22
where
φ
d
denotes the electrical potential at the OHP (i.e.,
the inner plane of the electrical diffuse layer). The charge
in the diffuse layer is given by averaging the concentra-
tions over the thickness of the electrical diffuse layer.
The electrical double layer problem can be finally
solved by using a final condition in the form of a global
electroneutrality condition for the electrical double layer
and the mineral surface. This condition implies that the