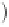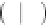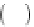Geoscience Reference
In-Depth Information
Bayesian analysis considers both the data vector,
d
, and
the model parameter vector,
m
, as random variables
defined by probability density functions (Mosegaard &
Tarantola, 1995; Gelman et al., 1996; Haario et al.,
2001). The objective of the inverse modeling process is
to update the information on
m
given
d
; Green
Another valid consideration for dropping the term
M
from the equations is that the division by the evidence
factor is basically a normalization process which is not
required to perform the inversion. The only exception
for this is if we want to explicitly compute the probability
for a given parameter in a particular interval. From the
final expression of Equation (5.19), the inverse problem
then can be solved by computing the expectation values
of
s func-
tions of the system,
K
; and prior knowledge of
m
.
'
), such as the mean, median, and the standard
deviation of
π
(
m
|
d
5.2.2 Algorithm
Now, we apply the Bayesian framework to estimate the
posterior probability density of the model parameters.
We chose the following vector of sevenmodel parameters:
m
) that can be considered as the final
or most likely values of the reconstructed model.
The formulation of
π
(
m
|
d
) is des-
cribed as follows. Assuming that the three quantities
are Gaussian distributed, their likelihood functions are
written as,
π
(
m
|
d
),
P
(
d
|
m
), and
P
0
(
m
=log
10
x
S
,log
10
z
S
,log
10
h
d
,
M
w
,
M
xx
,
M
xz
,
M
zz
T
where
x
s
and
z
s
denote the coordinates of the source,
h
d
represents
the thickness of the first layer, and the other parameters
represent the magnitude and the independent compo-
nents of the sourcemoment tensor. Note that the variables
involved in
1
dm
=
P
1 2
×
N
det
C
d
2
π
are independent variables. Then, the
Bayesian solution of the inverse problem is obtained by
combining the information from the data and the prior
information of the model parameters.
In a probabilistic framework, the objective of the
inverse modeling is to look for the maximum posterior
probability density,
m
1
2
d
−
T
C
−
1
d
exp
−
g
m
d
−
g
m
5 20
where
N
is the number of data, and the prior distribution
on the
M
model parameters is written as
,
M
), values computed from
the multiplication of a prior probability density of the
model parameters,
m
, in model
M
,
P
0
(
π
(
m d
1
P
0
m
=
1 2
×
M
det
2
π
C
m
m
M
), with the
1
2
m
−
m
prior
probability density of likelihood,
P
(
,
M
), correspond-
ing to the data fit. In our test, the data corresponds to the
seismic data alone or the seismic plus electrical data taken
together. We will note that
d m
T
C
−
m
exp
−
m
−
m
prior
5 21
To solve Equations (5.20) and (5.21), we need to set up
the forward modeling operator for the seismic and elec-
trical responses (based on the finite-element modeling of
the field equations described in the main text),
g
(
m
). We
also need to establish the prior values of the probability
distributions for the seven model parameters that we
want to recover,
m
prior
, and we need to define the covar-
iance diagonal matrices for the data,
C
d
, and the model,
C
m
, incorporating the uncertainties related to the data
and the prior model, respectively. The vector
d
=
d
S
,
d
E
T
is an
N
-vector consisting of the observed seis-
mic data,
d
S
, and electrical data,
d
E
. The data vector,
d
,is
defined in a way that the (
N
×
N
) matrix,
C
d
, is written as
a diagonal matrix with the inverse of the covariance for
the seismic and electrical data in the first and second set of
diagonal elements, respectively. This allows for the
weighting of the data according to the noise in the data.
This is especially important if the electrical data are nois-
ier than the seismic data.
m
Prior
is the prior vector of
model parameters. Using this approach, the posterior
probability density,
π
(
m d
,
M
), is obtained using Bayes
'
formula
,
M
=
P
dm
,
M P
0
m
M
π
md
5 17
P
d
M
where the denominator (the evidence) is defined as
P
d
M
=
P
dm
,
M P
0
m
M d
m
5 18
Assuming that the model
M
is certain, we can drop the
term
M
from Equations (5.17) and (5.18). If this is
the case, the posterior probability density,
π
(
m
|
d
,
M
), of
the model parameters
m
given the data
d
is written as
π
md
=
P
dm
P
0
m
5 19