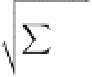Geoscience Reference
In-Depth Information
Table 4.4
Material properties used for the numerical
simulations corresponding to the case study #1.
4.4.3 The initial inverse solution
Because the number of the measurement points is much
less than the number of mesh elements of the model
where the source can be located (
N
<<
M
) (this is typical
of potential field problems), the inverse problem is
underdetermined. It is also ill posed and the solution is
nonunique. The nonuniqueness of the inverse problem
can be significantly reduced by using a regularization
approach to select a solution that minimizes both the data
misfit and, at the same time, carries a representation of
the model structure that is consistent with some prior
information (sparseness of the source distribution in this
case).
The inverse problem involves reconstructing the
spatial distribution of the volumetric source field (right-
hand side of Eq. 4.66) at each time
t
through the
optimization of the objective functions
Parameter Description
Unit U1
Unit U2
0.01 S m
−
1
0.1 S m
−
1
σ
Conductivity of the
medium
0.203 C m
−
3
3.49 C m
−
3
Q
V
Excess of charge
per unit pore volume
2650 kg m
−
3
2650 kg m
−
3
ρ
s
Bulk density of the
solid phase
1000 kg m
−
3
1000 kg m
−
3
ρ
f
Bulk density of the
fluid phase
ϕ
Porosity
0.25
0.10
36.5 × 10
9
Pa 6.9 × 10
9
Pa
K
s
Bulk modulus of the
solid phase
0.25 × 10
9
Pa 0.25 × 10
9
Pa
K
f
Bulk modulus of the
fluid phase
4.00 × 10
9
Pa 3.57 × 10
9
Pa
G
Shear modulus of the
frame
Bulk modulus of the frame 2.22 × 10
9
Pa 6.89 × 10
9
Pa
K
fr
2
2
,
2
2
+
10
−
12
m
2
10
−
16
m
2
obs
k
Low-frequency
permeability
C
=
W
d
Gs
−
ψ
λ
Λ
s
4 67
0
10
−
3
Pa s
10
−
3
Pa s
η
f
Dynamic viscosity of the
pore fluid
N
G
kj
2
,
Λ
= diag
4 68
i
−
1
Unit U1 simulates a sandstone, and unit U2 is used to simulate a
clayey sandstone.
where
G=PK
−
1
denotes the
N×M
matrix of the Green
functions. This matrix is computed as the product of
the inverse kernel matrix times a sparse selector operator
matrix
P
N
×
M
that contains a single 1 on each row in the
column that corresponds to the location of that receiver.
The rows of
G
can be computed effectively using reci-
procity, which involves computing the forward response
to a unit source located at each receiver. The vector
In the finite-element code COMSOL Multiphysics, the
governing equation of the forward electrical model can
be written at each time step as
Λ
represents an inverse-sensitivity weighting function that
accounts for distance from the receivers as well as the
resistivity structure,
s
is the vector containing the discre-
tized source current density terms
ψ
K
=s
,
4 66
where
K
is the kernel matrix that contains the
discrete form of the differential operator on the left
hand of Equation (4.66),
s
is a vector containing the
M
source current density terms
(
r
,
t
) with dimension
obs
is the observed electric potential vector at the
N
sensors, and
W
d
is a matrix that contains the information
about the expected noise in the data. The parameter
M
,
ψ
(
x
,
t
), and
ψ
is the vector
of electric potential observations at
the
N
receiver
λ
in Equation (4.67) corresponds to a trade-off parameter
between the two contributions of the cost function. In
other words, this term balances the relative influence
of the data misfit term,
C
d
=
W
d
Gs
locations.
At the boundaries of the domain, we used the
following boundary conditions: A Neumann boundary
condition is used at the interface between the model
and the padding layer. At the outer edge of the padding
layer, a Dirichlet boundary condition is used. The electric
potential at the outer edge of the padding layer tends
to zero, thus simulating an infinite domain (Dey &
Morrison, 1979).
2
2
, and the
−
ψ
obs
2
2
. It is called the regulariza-
model misfit term,
C
m
=
Λ
s
tion term.
In the following, we consider
W
d
to be diagonal with
each element on the diagonal being the inverse of the