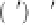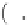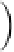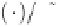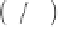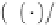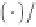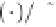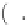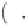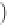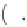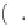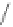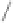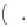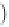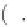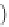Geoscience Reference
In-Depth Information
boundary conditions are adjusted to prevent these
reflections. A common approach to limit reflection at
the boundaries of the domain is to use the one-way wave
equation, based on the paraxial approximations of the
seismic wave equations (Clayton & Engquist, 1977). The
perfectly matched layer (PML) method is described later
as an alternativeway by Berenger (1994), first for electro-
magnetic problems and then for seismic problems (Chew
& Weedon, 1994; Zeng & Liu, 2001; Zeng et al., 2001).
With PML boundary layers, (almost) no reflection is
expected to occur at the interface between the physical
domain and the absorbing layer for any frequency and
any angle of incidence of the seismic waves.
In this topic, we use the convolutional perfectly
matched layer (C-PML) approach for our numerical
examples. The C-PML method, for first-order system of
partial differential equations, has been developed for
electromagnetic waves by Roden and Gedney (2000)
and in simulation of elastic wave propagation by Bou
Matar et al. (2005). This method can be extended for
second-order systems written in terms of displacements.
The main advantages of the C-PML approach over the
classical PML approach concern its numerical stability
and its high efficiency (Martin et al., 2008). Using the
concept of complex coordinates (Chew & Weedon,
1994) in the frequency domain (with a time dependence
of
e
−
i
ω
t
), the complex coordinate stretching variables are
x
i
min
−
x
i
π
f
0
+1 ,as
x
i
min
≥
x
i
,
L
0
α
i
=
π
f
0
,
as
x
i
min
≤
x
i
≤
x
i
max
,
x
i
−
x
i
max
L
0
π
f
0
+1 ,as
x
i
≥
x
i
max
,
4 25
where
c
is the highest of all of the velocities in the
domain,
R
= 1/1000 represents the amount of reflected
energy at the outer boundary of the PML,
L
0
is the
thickness of the PML, and
f
0
is the dominant frequency
of the source (see Section 4.1.3).
In the succeeding text, the derivative
x
i
can
be expressed in terms of the regular coordinate stretching
variables,
∂
∂
∂
∂
x
i
=
1
s
x
i
∂
∂
x
i
. Finally, after repla-
cing
x
i
and after some algebraic
manipulations, the reduced set of equations for the
modified poroelastic formulation is
∂
∂
x
i
by
∂
∂
−ω
2
ρ
s
w
u
+
θ
∇
p
=
∇
T
,
4 26
w
θ
w
s
x
2
0
θ
w
=
,
4 27
θ
w
s
x
1
0
s
w
s
w
s
x
1
s
x
2
,
ρ
=
ρ
4 28
T
11
T
12
T
21
T
22
T
=
,
4 29
x
i
T
11
=
λ
+
2
G
s
x
2
s
x
1
∂
u
1
∂
x
1
+
λ
∂
u
2
x
2
,
4 30
x
i
=
s
x
i
x dx
,
i
=1,2,
4 22
∂
0
T
22
=
λ
∂
u
1
∂
x
1
+
λ
+
2
G
s
x
1
s
x
2
∂
u
2
s
x
i
=
k
x
i
x
i
+
σ
x
i
x
i
α
x
2
,
4 31
∂
,
4 23
+
j
ω
x
i
s
x
1
s
x
2
∂
∂x
2
+
∂
u
1
u
2
∂x
1
T
12
=
G
,
4 32
where
σ
x
i
are positive real damping coefficients and
k
x
i
are real and positive-definite numbers that are equal
or larger than unity. In this paper, we consider
k
x
i
=1
to keep the waves continuous (see Collino & Tsogka,
2001, for details). To determine the value of the two
other damping coefficients, we use the following
formula:
α
x
i
,
T
21
=
G
∂
u
1
x
2
+
s
x
2
s
x
1
∂
u
2
,
4 33
∂
∂
x
1
s
x
1
s
x
2
M
p
+
2
∇
k
1
ω
∇
p
−
k
2
ω
ω
ρ
f
u
=
α
s
x
1
s
x
2
∇
u
,
4 34
k
ω
s
x
2
s
x
1
0
k
1
ω
=
,
4 35
0
k
ω
s
x
1
s
x
2
3
x
i
min
−
x
i
3
c
2
L
0
log
1
R
, s
x
i
min
≥
x
i
,
k
ω
s
x
2
0
L
0
k
2
ω
=
4 36
0
k
ω
s
x
1
0,
as
x
i
min
≤
x
i
≤
x
i
max
,
σ
i
=
3
3
c
2
L
0
log
1
R
x
i
−
x
i
max
L
0
For the electrical problem associated with the
electrokinetic conversions, we solve the following
modified equations:
,as
x
i
≥
x
i
max
,
4 24