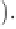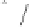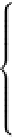Geoscience Reference
In-Depth Information
The parameters
Q
0
1
and
Q
0
2
denote the effective excess
charge (of the diffuse layer) per unit pore volume (in
Cm
−
3
) of the nonwetting and wetting fluids, respec-
tively. For water-saturated rocks,
Q
0
C
=
BK
u
3 156
H
=
K
u
+
4
3
G
3 157
2
can be directly com-
puted from the low-frequency permeability,
k
0
, of the
porous material. However, we assume that the excess
charge
Q
0
Equation (3.155) links various physical properties to
the amplitudes of coseismic electric fields that travel
along with seismic P-wave.
In this section, we extend this proportionality for a
medium saturated with two fluid phases. For this reason,
we solve the set of equations that govern seismoelectric
coupling by considering a compressional, pure harmonic
plane wave in 1D,
1
=0Cm
−
3
for the nonwetting phase, and
therefore, the seismoelectric conversion originates only
from the wetting phase. In this case, we write the current
density source as
Q
2
S
2
k
2
∇
in a homogeneous and isotropic
2
J
S
=
−
i
ω
p
2
-
ω
ρ
2
u
3 154
material:
The effect of water saturation on the excess electrical
charges per unit volume is developed by extending the
empirical relationship between the two charge density
parameters in unsaturated conditions. This is done by
substituting
Q
0
u
=
U
exp
ikx
−
ω
t
3 158
w
1
=
W
1
exp
ikx
−
ω
t
3 159
w
2
=
W
2
exp
ikx
−
ω
t
3 160
2
in water-saturated conditions for
Q
0
2
S
2
in unsaturated conditions (see Linde et al., 2007; Revil
et al., 2007).
E
=
E
0
exp
ikx
−
ω
t
3 161
where
U
and
W
1,2
are wave amplitudes,
is the angular
wave excitation frequency, and
k
=
k
r
+
ik
i
is a complex
wave number that includes an attenuation coefficient
as the phase slowness that can be defined as
s
=
k
r
ω
ω
3.2.4 The effect of water content on the
coseismic waves
Pride and Haartsen (1996) proposed a relationship of the
proportionality between electromagnetic fields and the
horizontal displacements of the grains. This proportional-
ity was observed in a set of seismic and seismoelectric
data acquired in the field by Garambois and Dietrich
(2001). To establish this relationship, the authors defined
the problem in the diffusive regime, a valid assumption
given the frequencies encountered in field measure-
ments. In the fully saturated conditions, the transfer
function for the P-wave was derived from the eigenvalue
response of an isotropic and homogeneous medium and
expressed in the low-frequency regime under the follow-
ing form:
.
The complete set of governing equations that described
the poroelastic problem (Eqs. 3.93, 3.99) may be reduced
to three vector equations as follows:
A
11
θ
1
A
22
θ
2
R
11
θ
1
−
R
22
θ
2
ρ
s
θ
s
0
−
0
R
11
2
−
ω
+
i
ω
θ
1
0
00
R
22
θ
1
ρ
1
θ
ρ
1
θ
0
1
1
ρ
2
θ
2
0
ρ
2
θ
2
a
12
θ
1
a
13
θ
2
a
11
U
W
1
W
2
0
0
0
a
22
θ
1
a
23
θ
2
+
k
2
a
2
s
=
3 162
a
23
θ
1
a
33
θ
2
a
3
s
−
ρ
f
ε
f
ζ
σ
f
μ
f
−
ρ
ρ
f
E
x
−
ω
C
H
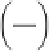
The existence of a solution to this equation requires
that the determinant of its coefficients must vanish.
The determinant can be formulated as
2
u
x
=
1
3 155
where
E
x
and
u
x
are the amplitudes of the horizontal
components of the electrical field and solid phase dis-
placement, respectively,
3
2
2
k
2
2
k
2
2
k
2
Q
3
ω
+
Q
2
ω
+
Q
1
ω
+
Q
0
=0
3 163
ε
f
is the fluid
'
s dielectric permit-
tivity,
σ
f
is the fluid
'
s electrical conductivity,
μ
f
is the
For a given frequency, the polynomial Equation
(3.163) of the dispersion has three complex roots, and
the wave number has six roots. However, only three
of these roots are physically possible. This implies the
fluid
is the zeta potential. Parameters
C
and
H
are the elastic moduli (as defined by Biot,
1962a, b) that are related to the undrained bulk modulus
and the Skempton coefficient as shown here:
'
s viscosity, and
ζ