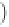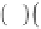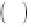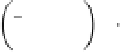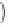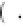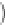Geoscience Reference
In-Depth Information
alternate formulation, we use a two-step technique. In
the first step, we apply the Fourier transform to the set
of equations to convert them into the frequency domain,
and then, in the second step, we conduct algebraic mani-
pulations to derive the formulations that are usable for
numerical processing. We start with the following for-
mulae, in the frequency domain:
For the solid phase, the momentum conservation equa-
tion (Newton
'
s law) and the total stress are expressed by
2
−
ω
ρ
T
u
+
ρ
1
w
1
+
ρ
2
w
2
+
θ
1
∇
p
1
+
θ
2
∇
p
2
=
∇
T
3 124
2
3
G
u
+
a
12
w
1
+
a
13
T
=
a
1s
−
∇
θ
1
∇
θ
2
∇
w
2
I
+2
G
e
R
ii
θ
3 125
2
−ω
ρ
i
u
s
+
ρ
i
w
i
+
i
ω
w
i
=
−∇
p
i
3 116
i
where
ρ
i
=
ρ
i
a
1s
=
a
11
+
a
12
+
a
13
3 126
A
ii
θ
θ
i
−
3 117
2
i
Following Biot (1962a, b), we can express the stress
-
Equation (3.116) can be used to express the filtration
displacement of each fluid,
w
i
, as a function of the pore
fluid pressure
p
i
and the displacement of
strain relations in an isotropic porous medium as
−
θ
1
p
1
=
a
2s
∇
u
+
a
22
θ
1
∇
w
1
+
a
23
the solid
θ
2
∇
w
2
3 127
phase
u
:
u
+
a
23
w
1
+
a
33
−
θ
2
p
2
=
a
3s
∇
θ
1
∇
θ
2
∇
w
2
3 128
2
w
i
=
−
k
i
ω
∇
p
i
−
ω
ρ
i
u
3 118
1
i
ωρ
i
+
Solving for
∇
w
1
and
∇
w
2
,
k
i
ω
=
−
3 119
R
ii
θ
2
i
∇
w
1
=
α
∇
u
+M
11
p
1
−
M
12
p
2
3 129
s1
which can be written as
w
i
=
k
i
∇
ρ
i
u
s
where
k
i
(
ω
)
is the frequency-dependent apparent permeability that is
similar to the one defined in Jardani et al. (2010) for the
seismoelectric problem in saturated conditions repre-
sented by
k
ω
(see Chapter 2). We can write
p
i
−
ω
2
∇
w
2
=
α
s2
∇
u
−
M
12
p
1
+M
22
p
2
3 130
Subsequently, we can rewrite the equations of motion
in terms of the three new unknown fields (
u
,
p
1
, and
p
2
)as
k
i
ω
i
1
2
k
i
=
=
3 120
−
ω
ρ
T
u
+
θ
1
∇
p
1
+
θ
2
∇
p
2
=
∇
T
3 131
R
ii
θ
ω
ω
2
ρ
i
−
ω
i
2
i
u
T
T
=
λ
s
∇
u I
+
G
∇
u
+
∇
3 132
For the solid phase, the momentum conservation
equation is written as
2
M
11
p
1
−∇
k
1
∇
p
1
-
ω
ρ
1
u
=M
12
p
2
−α
s1
∇
u
3 133
2
M
22
p
2
−∇
k
2
∇
p
2
−
ω
ρ
2
u
=
M
12
p
1
−
α
s
2
∇
u
3 134
2
i
=1
ρ
i
w
i
+
2
i
=1
θ
2
−
ω
ρ
T
u
+
∇
p
i
=
∇
T
3 121
i
s law applied
to the solid skeleton of the porous material. This equation
is similar to Newton
Equation (3.131) corresponds to Newton
'
We now discuss the elimination of the unknown vari-
ables,
w
i
, from these equations. We use the momentum
conservation equations for the two fluid phases written
in the frequency domain as follows:
'
s equation of elastic bodies except for
the coupling terms
p
i
, which represents the coupling
between the solid and fluid phases. The stress tensor
defined by Equation (3.132) corresponds to the stress
tensor with the porous material in vacuum (i.e., it corre-
sponds to the stress acting on the solid phase if the pore
fluid is replaced by vacuum). Equations (3.133) and
(3.134) are the nonlinear diffusion equations for the pore
fluid pressure of each fluid in which the effect of the
θ
i
∇
R
11
θ
2
−
ω
ρ
1
u
+
ρ
1
w
1
+
i
ω
w
1
=
−∇
p
1
3 122
1
R
22
θ
2
−
ω
ρ
2
u
+
ρ
2
w
2
+
i
ω
w
2
=
−∇
p
2
3 123
2
2