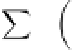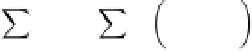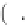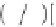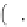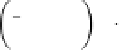Geoscience Reference
In-Depth Information
porous material and that a third P-wave that is developed is
a diffusive wave related to fluctuations in the pressure dif-
ference (capillary pressure) between the fluid phases. The
problem consisted of solving a set coupled equation with
three unknown vectors,
u
(the displacement vector field
of the solid phase), and
u
1
and
u
2
, the displacement vector
fields of the two immiscible fluid phases.
For the two fluid phases, the momentum conservation
equation is written as (Lo et al., 2005)
superscript
denotes the transpose of the matrix
and
G
denotes the shear modulus of the porous medium
frame.
Following the Biot
“
T
”
-
Frenkel theory for a single phase,
the linear stress
strain relations for an elastic porous
medium bearing two immiscible Newtonian fluids have
been generalized by Tuncay and Corapcioglu (1997)
using microscopic volume averaging:
-
−
θ
1
p
1
=
a
12
∇
u
+
a
22
∇
u
1
+
a
23
∇
u
2
3 91
2
u
i
∂t
2
+
i
∂
R
ii
∂
∂t
−
∂
u
i
u
∂t
ρ
i
θ
θ
∇
p
i
−
i
−
θ
2
p
2
=
a
13
∇
u
+
a
23
∇
u
1
+
a
33
∇
u
2
3 92
3 88
2
2
u
j
∂
2
u
∂
A
ij
∂
t
2
−
∂
−
t
2
=0,
i
=1,2
where
u
1
and
u
2
denote the displacements of the respec-
tive fluids. In this formulation,
p
1
and
p
2
represent the
infinitesimal changes of the nonwetting and wetting
pressures, respectively, where their linear relationships
with the volumetric strains (dilatations) of the solid
and two fluid phases depend on the elastic properties
of the solid matrix and on the properties of the two fluids.
To simplify the previous set of equations, we neglect the
inertial drag (
A
12
=
A
21
= 0) of the interactions of a fluid
with an adjacent fluid, and we introduce the average dis-
placement vector of a fluid relative to the solid phase
instead of the displacement of the fluid phase
i
given
by
w
i
=
j
=1
while for the solid phase, we have
2
u
∂
2
2
ρ
s
θ
s
∂
R
ii
∂
u
i
∂
t
−
∂
u
∂
t
2
+
p
i
∇
θ
i
+
t
i
=1
i
=1
3 89
2
2
2
u
j
∂
2
u
∂
A
ij
∂
t
2
−
∂
+
−∇
T
=0
t
2
i
=1
j
=1
The stress tensor is given by
u
.
For the two fluid phases, we have
θ
i
u
i
−
2
3
G
T
=
a
11
−
∇
u
+
a
12
∇
u
1
+
a
13
∇
u
2
I
+2
G
e
3 90
2
u
∂
2
w
i
∂
ρ
i
∂
t
2
+
ρ
i
A
ii
θ
∂
R
ii
θ
∂
w
i
∂
θ
i
−
−
=
−∇
p
i
,
i
=1,2
2
i
t
2
2
i
t
In these equations, the nonwetting fluid corresponds
to
i
= 1 (fluid 1), and the wetting fluid corresponds to
i
= 2 (fluid 2),
I
is the identity matrix, and
p
i
is the fluid
pressure of the fluid phases
i
. The
A
ij
coefficients are con-
stitutive coefficients that account for the effect of inertial
coupling, while the cross-coupling effects caused by iner-
tial drag are neglected (
A
12
=
A
21
= 0). The
R
ii
coefficients
denote the coefficients related to viscous drag, and
3 93
while for the solid phase, we have
2
u
∂
2
2
w
i
∂
2
ρ
s
θ
s
∂
A
ii
θ
i
∂
R
ii
θ
i
∂
w
i
∂
=
∇
t
2
+
t
2
+
T
3 94
t
i
=1
i
=1
ρ
i
and
ρ
s
are the mass densities of the fluid
i
and the solid,
respectively. In Equations (3.89) and (3.90), the param-
eter
We use Equation (3.93) to rewrite Equation (3.94) as
θ
s
is the volume fraction of the solid phase, and the
parameter
2
u
∂
2
i
=1
ρ
i
∂
2
w
i
∂
2
i
=1
θ
i
∇
ρ
T
∂
t
2
+
+
p
i
=
∇
T
3 95
θ
i
is the volume fraction of the
i
th fluid phase.
Note that the volume fraction of the fluid phase may be
written in terms of the porosity
t
2
ϕ
and the fluid saturation
2
3
G
u
+
a
12
w
1
+
a
13
T
=
a
1
s
−
∇
θ
1
∇
θ
2
∇
w
2
I
+2
G
e
as
S
i
. The tensor
T
denotes the stress tensors associ-
ated with the solid phase, and
a
nm
(
n
,
m
=1,2,3) are elastic
coefficients where their cross terms are symmetric, that
is,
a
nm
=
a
mn
. The solid phase strain tensor of the elastic
skeleton is defined by
e=
1 2
θ
i
=
ϕ
3 96
with
u
T
a
1
s
=
a
11
+
a
12
+
a
13
3 97
∇
u
+
∇
, where the