Biomedical Engineering Reference
In-Depth Information
This system of equations is known as the
van der Pol oscillator
, and it de-
scribes the time evolution of two variables
u
and
v
. In order to begin our
discussion of its solutions, let us notice that two curves in the phase space
(
u, v
) delimit boundaries between regions with different behavior. Within the
region of the phase space in which
v>
1
/
3
cu
3
+(
β
−
b
)
u
,
u
increases, since
˙
u>
0, while
u
decreases if
v<
1
/
3
cu
3
+(
β
b
)
u
. The variable
v
,onthe
other hand, decreases whenever
u>
0, and increases in the region of the
phase space where
u<
0. The curves
−
1
3
cu
3
+(
β
v
=
−
b
)
u,
(4.8)
u
= 0
(4.9)
are known as the
nullclines
of the system. Let us use these curves as a back-
bone for our understanding of the dynamics displayed by these equations,
and let us assume that the constant
k
in them is small.
We start with an initial condition such that
v
is larger than
f
(
u
)
−
b
)
u
+1
/
3
cu
3
(see (4.8)). According to (4.6),
u
increases. A rapid excursion in
phase space then occurs until the system reaches the branch with a positive
slope of
v
=
f
(
u
) and with positive
u
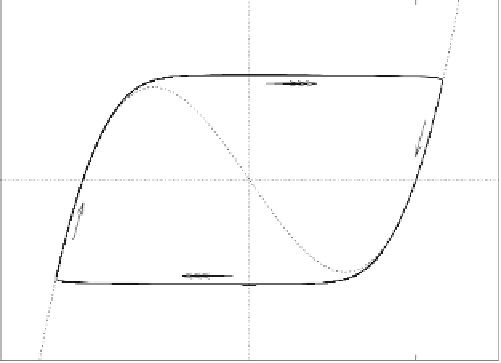
(see Fig. 4.3). We say that this excursion
is fast, because we compare it with the slow evolution of
v
:
v
is small since
k
is small.
≡−
(
β
0.5
0
-0.5
-1
0
1
u
(arb. units)
Fig. 4.3.
The dynamics of the van der Pol oscillator ((4.6) and (4.7)). The phase
space plot illustrates the time evolution of the system (
solid line
), which alternates
between slow excursions close to the nullcline
u
=0(
dashed line
), and fast jumps
between branches of the nullcline