Biomedical Engineering Reference
In-Depth Information
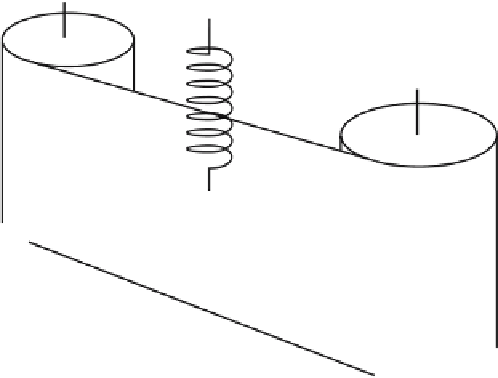
Fig. 4.1.
A system performing harmonic oscillation: a small mass attached to a
spring. The mass is subjected to a force by the spring, whose characteristic feature
is that it is
linearly restitutive
. This means that, if the mass is displaced from its
equilibrium position, the spring will tend to restore it to that position by exerting
a force proportional to the displacement (that is, the force is twice as large if the
mass is displaced twice as far). Once displaced and released, the mass will oscillate
back and forth around the equilibrium position owing to the restitution force. The
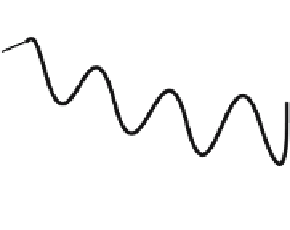
record left on the paper is a trace of the harmonic oscillation
return trip towards the initial position, where the story begins all over again.
What determines the frequency of the oscillations of this mass attached to
a spring? The strength of the restitution force for a given departure from
the equilibrium position. This can be described by means of a restitution
coe
cient
K
.If
x
represents the system's departure from equilibrium, the
restitution force is
F
spring
=
−Kx
, and the dynamics of the system can be
described by
M
d
2
x
dt
2
=
−
Kx,
(4.1)
or, as a two-dimensional system of first-order equations,
x
=
y,
K
M
x,
(4.2)
with the solution
x
(
t
)=
A
cos(
ωt
+
φ
), where
ω
=
K/M
,
M
is the mass
and
A
and
φ
are determined by the initial conditions. A dot on top of a
variable is a shorthand notation for the time derivative.
However, not many of us have seen an oscillating system displaying this
behavior for a long time. If we play with a spring, we shall probably see that
after a few oscillations, it will stop. Another system which, in principle, can
y
=
−