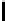Image Processing Reference
In-Depth Information
defined by such distance functions. Considering the hyperspheres formed by
d(N(·)), we get two more measurable quantities, namely the volume of the
sphere and the area of its surface. In discrete point space, the meaning of such
hyperspheres and their corresponding volumes and surface areas are analyzed
in this section.
A hypersphere H of a given radius r around the origin 0 is the set of
points whose distance measure from 0 is less than or equal to r. The set of
points whose distance measure from 0 is exactly equal to r is defined as the
surface S of the sphere. The number of points in H gives us the volume of the
hypersphere, and that of S, the surface area.
For example, in 2-D, the disk (of radius r) of City Block distance is an
isothetic diamond with vertices at {(±r,0),(0,±r)}. It has an area of 2r
2
+
2r + 1 and a perimeter of 4r. Similarly, the disk of Chessboard distance is
isothetic square with vertices at {(±r,±r)}, area 4r
2
+ 4r + 1, and perimeter
8r. Also, the diamond is totally contained within the square.
Likewise in 3-D, lattice, d
18
and grid distances define three convex digital
solids with the following properties (Table 2.8):
TABLE 2.8: Properties of hyperspheres of common distances in 2-D and
3-D.
Distance
Vertices
Perimeter /
Area /
Surface Area
Volume
2r
2
+ 2r + 1
City Block
{(±r, 0), (0, ±r)}
4r
4r
2
+ 4r + 1
Chessboard
{(±r, ±r)}
8r
24r
2
+ 2
18r
3
+ 12r
2
+ 6r + 1
Lattice
{(±r, 0, 0), (0, ±r, 0), (0, 0, ±r)}
20r
2
− 4r + 2
3
r
3
+ 8r
2
+
1
3
r + 1
d
18
{(±r, ±r, 0), (±r, 0, ±r),(0, ±r, ±r)}
20
4r
2
+ 2
3
r
3
+ 2r
2
+
3
r + 1
Grid
{(±r, ±r, ±r)}
4
In this section we present closed-form expressions for volumes and sur-
faces of hyperspheres. Using absolute and relative volumetric and surface error
measures, we also study how well these digital hyperspheres approximate the
Euclidean hypersphere.
2.5.1 Notions of Hyperspheres
Definition 2.29. S(N(·);r) is the hypersurface of radius r in n-D for
neighborhood set N(·). It is the set of n-D grid points that lie exactly at a
distance r, r ≥ 0, from the origin when d(N(·)) is used as the distance.
S(N(·);r) = {x : x ∈ Z
n
,d(x;N(·)) = r}
The surface area surf(N(·);r) = ||S(N(·);r)|| of a hypersurface
S(N(·);r) is defined as the number of points in S(N(·);r).
€