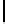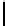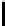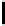Image Processing Reference
In-Depth Information
TABLE 2.4: m-Neighbor Norms in 2-D and 3-D.
d
m
(u)
n
m
Distance
d
1
=|u
1
|+|u
2
|
1
City Block
d
2
=max(|u
1
|,|u
2
|)
2
2
Chessboard
d
1
=|u
1
|+|u
2
|+|u
3
|
1
Grid
l
m
d
2
=max(|u
1
|,|u
2
|,|u
3
|,
|u
1
|+|u
2
|+|u
3
|
2
3
2
d
18
)
d
3
=max(|u
1
|,|u
2
|,|u
3
|)
3
Lattice
Let us consider an example at this point.
Example 2.10. Table 2.4 lists the m-Neighbor norms in 2-D and 3-D.
€
We know that in 2-D, City Block distance between two pixels is always
greater than the Chessboard distance. A similar result holds in n-D. ∀u ∈ Z
n
,
the values of the m-Neighbor norms are ordered in a non-increasing sequence
(for increasing m). That is:
d
1
(u) ≥ d
2
(u) ≥···≥ d
i
(u) ≥ d
i+1
(u) ≥ ... ≥ d
n
(u).
The following is proved in [60].
Lemma 2.4. ∀u ∈ Z
n
, d
r
(u) ≥ d
s
(u), ⇐⇒ r ≤s.
Lemma 2.5. ∀x,y ∈ Z
n
, x and y are r-neighbors iff d
r
(x,y) = 1 and
d
s
(x,y) > 1, ∀s,s < r.
€
Corollary 2.3. ∀x,y ∈ Z
n
are O(r)-adjacent neighbors iff d
r
(x,y) = 1.
€
2.3.1.1
Length of Shortest Path
We adopt the generic shortest path Algorithm 2 and adapt it for O(m)-
paths. Note the choice of the next point in this case with reference to the
general discussions on such a choice in Section 2.2.2.1.
At termination, length gives the number of iterations of the while loop,
which is the same as the number of points traced. In the following theorem,
we show that this is also given by the O(m)-neighbor distance function. (For
details of the proof, see [60]).
Theorem 2.4. d
m
gives the length of shortest O(m)-path between two points.
That is, ∀u,v ∈ Z
n
,
d
m
(u,v) = |Π
∗
(u,v;m : n)|.
Proof. We use the path tracing Algorithm 3 for the proof. There are two parts: