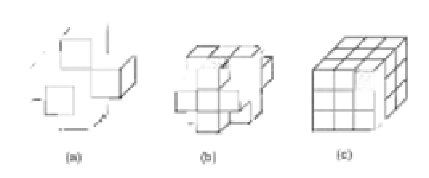Image Processing Reference
In-Depth Information
Reprinted from Sadhana 18(1993), P. P. Das and B. N. Chatterji,
Digital Distance Geometry: A Survey
, 159-187,
Copyright (1993), with permission from Indian Academy of Sciences.
FIGURE 2.2: Neighborhoods of a point in 3-D.
2.2.2 Digital Paths
Having introduced the underlying graph for the digital space with the
notions of adjacency through neighborhood sets, we are now ready to span
paths between pairs of points in n-D.
Definition 2.9. Given a neighborhood set N(·), a digital path Π(u,v;N(·))
between u,v ∈ Z
n
, is defined as a sequence of points in Z
n
where all pairs of
consecutive points are neighbors. That is,
Π(u,v;N(·)) : {u = x
0
,x
1
,x
2
,...,x
i
,x
i+1
,...,x
M−1
,x
M
= v}
∈ Z
n
and x
i+1
such that ∀i,0 ≤i < M, x
i
,x
i+1
∈N(x
i
).
€
Definition 2.10. The length of a digital path denoted by |Π(u,v;N(·))|,
is defined as
M−1
i=0
− x
i
). Usually there are many paths from u to v
and the path with the smallest length is denoted as Π
∗
(u,v;N(·)). It is called
the minimal path or shortest path.
If the neighborhood costs are all unity, then the length of the minimal path
is given by |Π
∗
(u,v;N(·))| = M. It is the number of points we need to touch
after starting from u to reach v.
δ(x
i+1
€
If the context of the neighborhood set is clear, we may simply refer to a
path by Π(u,v). If u = 0, the path is marked as Π(v;N(·)) or Π(v).
Interestingly, unlike Euclidean geometry, the shortest path between two
points in the digital grid is often not unique. That is, there are multiple paths
having the same minimum length. Hence, we usually talk about a shortest
path rather than the shortest path.
Example 2.4. We explore O(m)-neighbor (Table 2.1) paths in low dimensions
[60]. Neighborhood set N(·) is represented simply by m.
2-D
: Consider
u = (2, 3)
and
v = (5, 8)
.