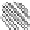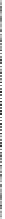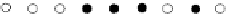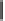Image Processing Reference
In-Depth Information
(a)
(b)
FIGURE 1.21: Transformation of a point set (denoted by dark points) in a
digital grid to an analog form (a) (4,8), and (b) (8,4). In this example, the
set of points is the same for both the grids.
that each of its smaller sides is of length 1, and the hypotenuse is of length
√
2. Typical examples of such conversion are shown in Fig. 1.21 (a) and (b).
For the same point set, the Euler number may differ. In this example in (4,8)
grid, it is 1 (2 components and 1 hole). In an (8,4) grid, the Euler number is
−1 (1 component and 2 holes).
Various methods are advanced to compute the Euler number using the
local features of a picture. In [94], it has been shown that the Euler number
could be computed by considering the 2 × 2 subsets of a digital grid. Such a
unit is referred as a quad cell. There could be six classes of quad structure out
of sixteen arrangements of foreground and background pixels. Four of these
classes are formed by the presence of a specific number of foreground points,
unless they are linearly inseparable from background points. There are two
types of inseparable configurations, each forming diagonals in a quad structure
with two background and two foreground points. Typical configurations of
these six classes are shown in Fig. 1.22.
Let Q
i
, i = 1,2,3, and 4 denote the classes corresponding to equivalent
configurations of Fig. 1.22 (a)-(d), and Q
d
denote a configuration of Fig. 1.22
(e) or (f). In that case, the Euler number E
8
in an (8,4) grid is given by the
following expression:
E
8
=
1
4
(n(Q
1
)−n(Q
3
)−2n(Q
D
))
(1.7)
where n(.) denotes the number of quads in that class in a digital grid. Similarly,
the Euler number E
4
in a (4,8) grid is expressed as follows:
E
4
=
1
4
(n(Q
1
)−n(Q
3
) + 2n(Q
D
))
(1.8)