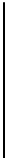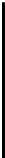Image Processing Reference
In-Depth Information
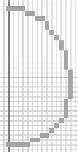
(a) A
discon-
nected
digital
curve.
(b) A
connec-
ted but
reducible
digital
curve.
(c) An
irred-
ucible
digital
curve.
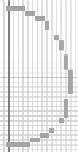
(d) A closed and
irreducible digital
surface, S.
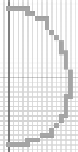
(e) An open and
irreducible dig-
ital surface, S
′
,
obtained by parti-
tioning S with the
horizontal
(f) Another open
and irreducible
digital surface,
S
′′
, obtained by
partitioning S
′
with the vertical
plane Π
′′
: x = a.
plane
Π
′
: y = c.
FIGURE 7.9: An illustration of connectivity and irreducibility of digital
curves and surfaces. (See color insert.)
Reprinted from
International Journal of Arts and Technology
,
4
: 196-215, G. Kumar et al., Copyright 2011, with
permission from Inderscience Publishers.
1.3.3.2 of Chapter 1). In order to generate a digital surface of revolution, S,
we consider a digital curve segment G as the digital generatrix, as shown in
Fig. 7.7. The digital generatrix may be taken as input, either as a sequence of
chain codes or as a sequence of control points. Given m(> 4) control points
as input, the digital generatrix is considered as the digital irreducible curve
segment that approximates the sequence of m−3 uniform non-rational cubic
B-spline segments interpolating the sequence of these control points [84, 99].
The reasons for B-spline interpolation of the generatrix is its unique character-
istic of having both parametric and geometric continuities, which ensure the
smoothness and the optimal exactness of the fitted curve against the given set
of control points. In addition, a local change (insertion/deletion/repositioning)
of control point(s) has only a local effect on the shape of the digital generatrix
(and a local effect on the generated surface, thereof). This, in fact, simulates
the local effect of a potter's hand rolling and maneuvering the clay on his
rotating wheel (Fig. 7.8).
Using the same notation discussed before, each point in N
k
(p) is said to be
a k-neighbor of p (k ∈{4,8} if p ∈ Z
2
and k ∈{6,26} if p∈ Z
3
). We consider
k = 8 and k = 4 in Z
2
, and k = 26 and k = 6 in Z
3
. If a connected digital
set S is such that S := Z
2
S(Z
3
S) contains at least two points, p ∈ S
and q ∈ S, which are not k-connected, then S is said possess a hole. A hole
H is a finite and maximal subset of S such that every pair of its points are
k-connected and none of its points is k-connected with any point from S H.
Clearly, S contains h − 1(h > 1) holes if and only if S contains at least h
points, namely, p
1
, p
2
,..., p
h
, no two of which are k-connected.
If S ⊂ Z
2
(Z
3
) is a connected digital set containing exactly one hole, namely
H, then S is said to be a closed digital curve (surface), of possibly arbitrary