Distance Functions in Digital Geometry - Digital Geometry in Image Processing - page 72

2.5.5.2 Special Cases of Hyperspheres in 2-D and 3-D

Next we take a deeper look into the disks (or spheres) in 2-D and 3-D for a
subclass of hyperoctagonal distances where the N-Sequence B is intrinsically
sorted (see Definition 2.22), that is, B = S(B). Examples of these disks and
spheres are shown in Figs. 2.11 and 2.12, respectively.
Under this condition, we show that the vertices are nicely approximated
and compact forms for the perimeter, area, volume, and shape feature exist.
Approximations of Vertices in 2-D and 3-D
We start by approximating the vertices in 2-D (digital disks) and 3-D (digital
spheres). The approximations are used to compute various properties of the
digital disks (spheres), and further to identify the best digital approximate
to the Euclidean metric. We present these approximate expressions for the
coordinates of the vertices in Theorems 2.26 [151] and Theorem 2.27 [154].
B being sorted, in 2-D, we write B as a doublet, B=[α 1 ,α 2 ] = {1 α 1 ,2 α 2 }
and α 1 +α 2 = p. If we approximate the vertex x(r) ∈ Σ n , of H(B;r), by x(r)
where x = r, rα 2

p

, the difference between x(r) and x(r) is bounded by the
following theorem from [151].

Theorem 2.26. For any r > 0 and for any sorted B, we have
1. r−x 1 (r) = 0;

p
4

p even

− α p

2. 0 ≤

rα 2
p

≤ €

−x 2 (r) ≤ α 1

(p 2 −1)
4p

p odd

(a) (b) (c)

(d) (e) (f)

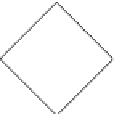
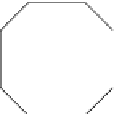
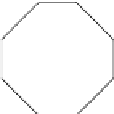
FIGURE 2.11: Digital circles of 2-D octagonal distances for sorted N-
Sequences: (a) {1}, (b) {1,2}, (c) {1,1,2}, (d) {1,1,1,2}, (e) {1,2,2}, and (f)
{2}.

Similarly, in 3-D, we write a sorted B as a triplet, B=[α 1 ,α 2 ,α 3 ] =
{1 α 1 ,2 α 2 ,3 α 3 } and α 1 +α 2 +α 3 = p. If we approximate the vertex x(r) ∈ Σ n ,