Introduction - On Statistical Pattern Recognition in Independent Component Analysis Mixture Modelling - page 9

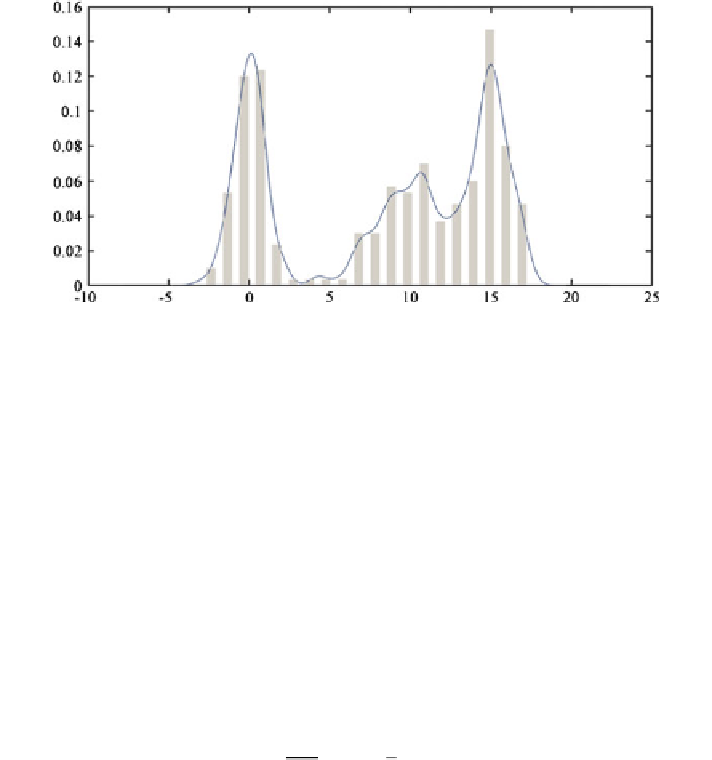
Fig. 1.4 Density estimation for univariate data

Table 1.1 shows the definition of some kernels used in non-parametric density
estimation.
There are no significant differences among the various kernels to estimate an
optimal window width ð h opt Þ on the basis of minimizing the approximate mean
integrated square error. Thus, it is suggested to base the choice of the kernel, for
example, on the degree of differentiability required or the computational burden
involved. The problem of choosing how much smoothness is required is of crucial
importance in density estimation. There are several methods proposed to estimate
h opt , for instance, subjective choice, reference to a standard distribution, least-
squares cross-validation, likelihood cross-validation, the test graph method, and
internal estimation of the density roughness 0 [ 37 ].
The kernel estimator as a sum of bumps centred at the observations for mul-
tivariate data is defined by the following expression

nh d X

n

f ð x Þ¼ 1

1
h ð x X i Þ

K ð 1 : 6 Þ

i ¼ 1

The kernel function K ð x Þ is a function defined for d-dimensional x, satisfying
R R d K ð x Þ dx ¼ 1 : K will be usually a radially symmetric unimodal probability
density function, for example the standard multivariate normal density function

K ð x Þ¼ð 2p Þ d = 2 e 2 x T x ð 1 : 7 Þ

The use of a single smoothing parameter K in Eq. ( 1.6 ) implies that the version
of the kernel placed on each data point is scaled equally in all directions. If the
variance of the data points is very much higher in some of the coordinate direc-
tions and a pre-scale step is not done, a vector or matrix of smoothing parameters
should be applied. However, if a pre-scale step is done, the Eq. ( 1.6 ) could be
applied using a single smoothing parameter.